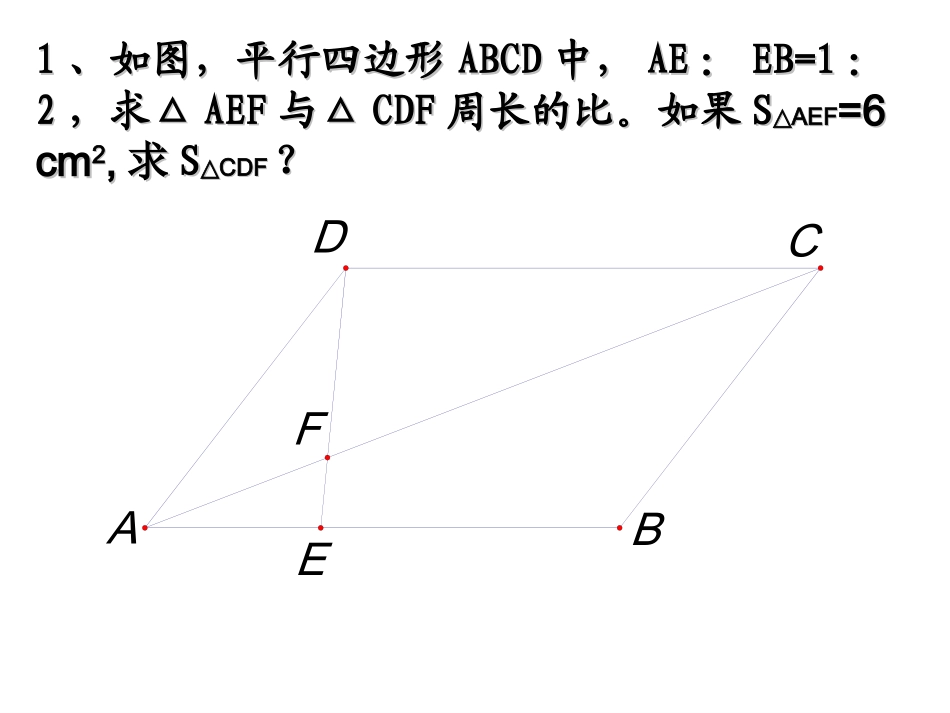
相似三角形应用举例((11)相似三角形对应的比等于)相似三角形对应的比等于相似比相似比..相似三角形相似三角形((多边形多边形))的性质的性质::((33)相似)相似面积面积的比等于的比等于相似比的平方相似比的平方..多边形多边形多边形多边形((22)相似)相似周长周长的比等于的比等于相似比相似比..三角形三角形三角形三角形高线高线角平分线角平分线中线中线复习回顾11、如图,平行四边形、如图,平行四边形ABCDABCD中,中,AEAE::EB=1EB=1::22,求△,求△AEFAEF与△与△CDFCDF周长的比。如果周长的比。如果SSAEF△AEF△=6=6cmcm22,,求求SSCDF△CDF△??FBCDAE2、△ABC中,DE∥BC,EF∥AB,已知△ADE和△EFC的面积分别为4和9,求△ABC的面积。FEDCBA33、如图,、如图,SS□□ABCDABCD=2008cm=2008cm22,点,点EE是平行四边形是平行四边形ABCDABCD的边的边ABAB的延长线上一点,且,那么的延长线上一点,且,那么SS△BEF△BEF==??ABBE41FDCABE44、如图、如图,,在△在△ABCABC中,点中,点DD、、EE分别是分别是ABAB、、ACAC的中点。的中点。DCBOAE(3)(3)若若SSDOE△DOE△=1cm=1cm22,,求求SSOBC△OBC△,,SSOEC△OEC△和和SSABC△ABC△..(1)(1)找出图中的各对相似三角形;找出图中的各对相似三角形;(2)(2)各对相似三角形的相似比各对相似三角形的相似比分别是多少?面积的比呢?分别是多少?面积的比呢?55、如图,、如图,ABCDABCD中,中,EE为为ADAD的中点,若的中点,若SABCD=1SABCD=1,则图中阴影部分的面积为(),则图中阴影部分的面积为()AA、、BB、、CC、、DD、、31516181BAEDCFB问题1.在同一时刻物体的高度与它的影长成正比例.在某一时刻,有人测得一高为1.8米的竹竿的影长为3米,某一高楼的影长为60米,那么高楼的高度是多少米?解:即高楼的高度为36米。6038.1x则有36得x解米,设高楼的高度为x因为在同一时刻物体的高度与它的影长成正比例2、如图,有一路灯杆AB(底部B不能直接到达),在灯光下,小明在点D处测得自己的影长DF=3m,沿BD方向到达点F处再测得自己得影长FG=4m,如果小明得身高为1.6m,求路灯杆AB的高度。DFBCEGA3.为了测量路灯(OS)的高度,把一根长1.5米的竹竿(AB)竖直立在水平地面上,测得竹竿的影子(BC)长为1米,然后拿竹竿向远离路灯方向走了4米(BB‘),再把竹竿竖立在地面上,测得竹竿的影长(B‘C‘)为1.8米,求路灯离地面的高度.hSACBB'OC'A'PDQBCA4.4.如图,小华在晚上由路灯如图,小华在晚上由路灯AA走向路灯走向路灯BB,当他走到,当他走到点点PP时,发现他身后影子的顶部刚好接触到路灯时,发现他身后影子的顶部刚好接触到路灯AA的的底部,当他向前再步行底部,当他向前再步行12m12m到达点到达点QQ时,发现他身时,发现他身前影子的顶部刚好接触到路灯前影子的顶部刚好接触到路灯BB的底部,已知小华的的底部,已知小华的身高是身高是1.60m1.60m,两个路灯的高度都是,两个路灯的高度都是9.6m9.6m,设,设APAP=x(m)=x(m)。。(1)(1)求两路灯之间的距离;求两路灯之间的距离;(2)(2)当小华走到路灯当小华走到路灯BB时,他在路灯下的影子是多少?时,他在路灯下的影子是多少?5.如图:小明想测量一颗大树AB的高度,发现树的影子恰好落在土坡的坡面CD和地面CB上,测得CD=4m,BC=10m,CD与地面成30度角,且测得1米竹杆的影子长为2米,那么树的高度是多少?CABD6、兴趣小组的同学要测量树的高度,在阳光下,一名同学测得一根长为1米的竹竿的影长为0.4米,同时另一名同学测量树的高度时,发现树的影子不全落在地面上,有一部分落在教学楼的第一级台阶上,测得此影子长为0.2米,一级台阶高为0.3米,如图所示,若此时落在地面上的影长为4.4米,则树高为()A.11.5米B.11.75米C.11.8米D.12.25米例1:如图,为了估算河的宽度,我们可以在河对岸选定一个目标作为点A,再在河的这一边选点B和C,使AB⊥BC,然后,再选点E,使EC⊥BC,用视线确定BC和AE的交点D.此时如果测得BD=120米,DC=60米,EC=50米,求两岸间的大致距离AB.ADCEB学.科.网解:因为∠ADB=∠EDC,∠ABC=∠ECD=90°,所以△ABD∽△ECD,答:两岸间的大致距离为100米.DC...