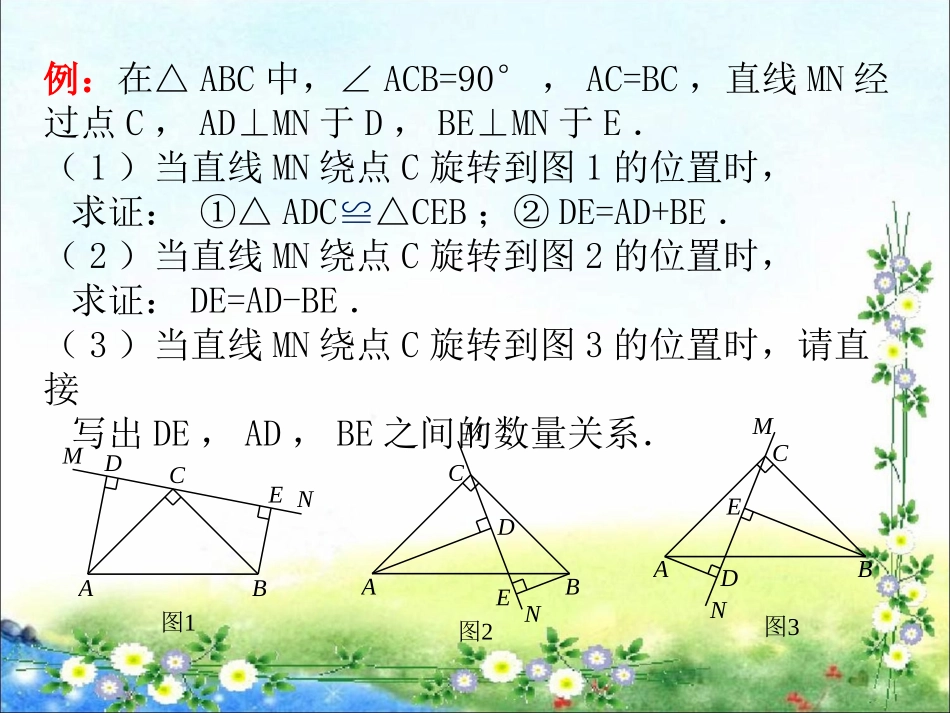
“变式训练”案例遂平县初中数学工作坊•以“变式教学”为研究平台,培养和发展学生的学习兴趣,调动学生的学习积极性,开发学生的思维,挖掘学生潜力,它能做到结构清晰、层次分明,使优、中、差的学生各有所得,尝试到成功的乐趣,并激发学生的学习热情,达到举一反三、触类旁通的效果,使他们的应变能力得以提高,进而提高教学质量。•在初中数学的教学过程中,老师经常会发现一种现象,很多学生对一种固定的题目模式较容易掌握,而对较灵活的题型缺乏理解、感知,改变已知条件,变换了图形位置后就束手无策,学生的思维常常局限于一些固定的框框里,以致产生厌学,缺乏自信心。例:在△ABC中,∠ACB=90°,AC=BC,直线MN经过点C,AD⊥MN于D,BE⊥MN于E.(1)当直线MN绕点C旋转到图1的位置时,求证:①△ADC≌△CEB;②DE=AD+BE.(2)当直线MN绕点C旋转到图2的位置时,求证:DE=AD-BE.(3)当直线MN绕点C旋转到图3的位置时,请直接写出DE,AD,BE之间的数量关系.图1BNECDMA图2ACDEMNB图3ABCDEMN(1)当直线MN绕点C旋转到图1的位置时求证:①△ADC≌△CEB;②DE=AD+BE.321AMDCENB∵∠ACB=90°∴∠1+∠2=90°∵AD⊥MN,BE⊥MN∴∠ADC=∠CEB=90°∴∠3+∠2=90°∴∠1=∠3在△ADC和△CEB中∠ADC=∠CEB,∠1=∠3,AC=CB证明:∴△ADC≌△CEB∴AD=CE,DC=EB∴DE=CE+DC=AD+BE(AAS)(2)当直线MN绕点C旋转到图2的位置时求证:DE=AD-BE.21BNMEDCA证明:∵∠ACB=90°∴∠1+∠2=90°∵AD⊥MN,BE⊥MN∴∠ADC=∠CEB=90°∴∠CBE+∠2=90°∴∠1=∠CBE在△ADC和△CEB中∠ADC=∠CEB,∠1=∠CBE,AC=CB∴△ADC≌△CEB(AAS)∴AD=CE,DC=EB∴DE=CE-DC=AD-BE(3)当直线MN绕点C旋转到图3的位置时,请直接写出DE,AD,BE之间的数量关系.321NMEDCBA解:DE=BE-AD,理由如下:∵∠ACB=90°∴∠1+∠2=90°∵AD⊥MN,BE⊥MN∴∠ADC=∠CEB=90°∴∠3+∠2=90°∴∠1=∠3在△ADC和△CEB中∠ADC=∠CEB,∠1=∠3AC=CB∴△ADC≌△CEB(AAS)∴AD=CE,DC=EB∴DE=DC-CE=BE-AD练习:如图1,四边形ABCD是正方形,AB=BC,∠B=∠BCD=90°,点E是边BC的中点,∠AEF=90°,EF交正方形外角∠DCG的平分线CF于点F.(1)求证:AE=EF(提示:在AB上截取BH=BE,连接HE,构造全等三角形,经过推理使问题得到解决).(2)如图2,如果把“点E是边BC的中点”改为“点E是边BC上(除B,C外)的任意一点”,其他条件不变,那么结论“AE=EF”仍然成立吗?说明理由.(3)如图3,点E是BC的延长线上(除C点外)的任意一点,其他条件不变,结论“AE=EF”是否成立?说明理由.GABCDFE图1EFDCBAG图2EFDCBAG图3欢迎指导,谢谢!