4.5相似三角形的性质及其应用(2)VIP免费

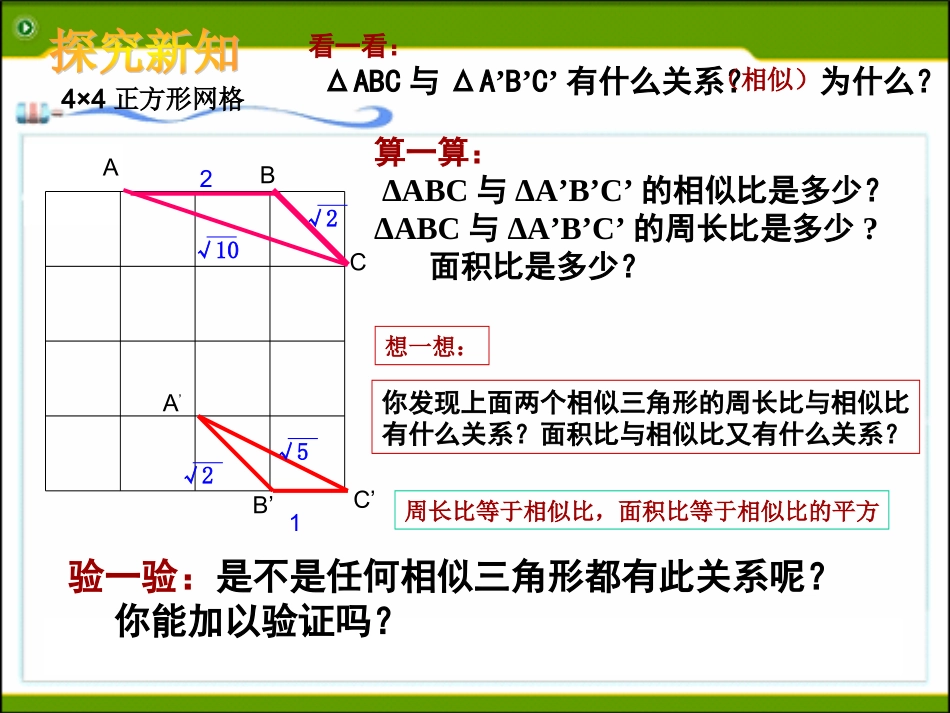
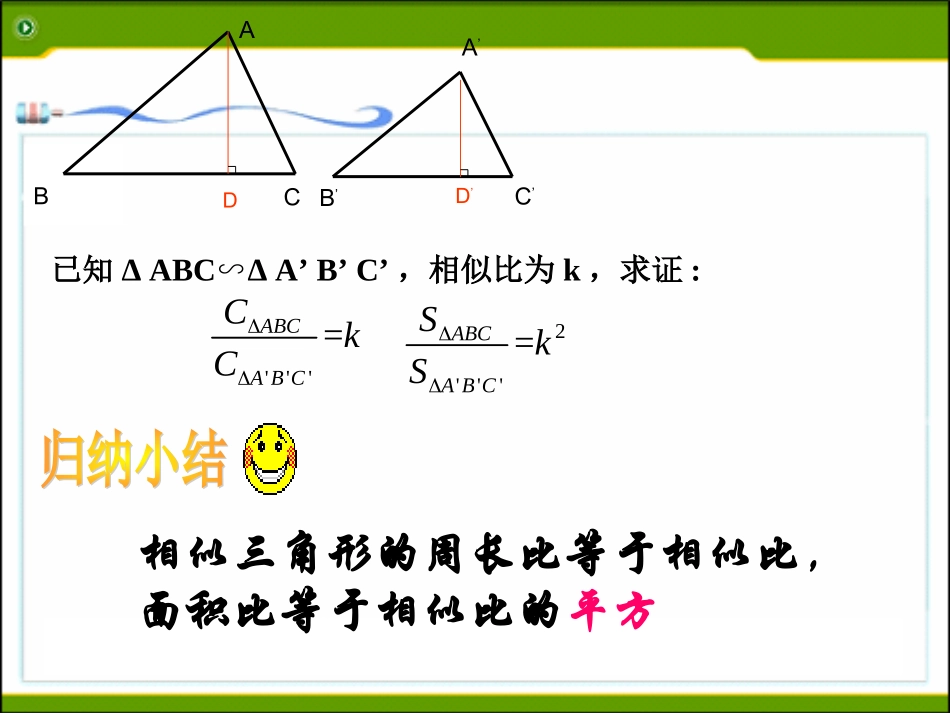
新浙教版数学九年级（上）4.5相似三角形的性质及其应用（2）算一算：ΔABC与ΔA’B’C’的相似比是多少？ΔABC与ΔA’B’C’的周长比是多少?面积比是多少？4×4正方形网格看一看：ΔABC与ΔA’B’C’有什么关系？为什么？验一验：是不是任何相似三角形都有此关系呢？你能加以验证吗？想一想：你发现上面两个相似三角形的周长比与相似比有什么关系？面积比与相似比又有什么关系？（相似）周长比等于相似比，面积比等于相似比的平方√102√21√5√2ABCA’C’B’ABCA’B’C’DD’相似三角形的周长比等于相似比，面积比等于相似比的平方已知ΔABC∽ΔA’B’C’，相似比为k，求证:'''=ABCABCCkC2'''=ABCABCSkS•已知：如图，△ABC∽△A’B’C’,△ABC与△A’B’C’的相似比是k,AD、A’D’是对应高。•求证：kDAAD''ABCB’A’C’DD’证明：kBAABDAAD'''' △ABCA’B’C’∽△∴∠B=B’∠∴∠ABD=A‘B’D‘=90∠O∴△ABDA’B’D’∽△两个相似三角形的对应高之比等于相似比。巩固提问:我们已经学习相似三角形的性质有哪些？1、相似三角形对应角相等。2、相似三角形对应边成比例。3、相似三角形的周长之比等于相似比；BCABCA´´´4、相似三角形的面积之比等于相似比的平方。5、相似三角形的对应高线、中线、角平分线之比等于相似比。1．(知识点1)若△ABC∽△DEF，△ABC与△DEF的相似比为12∶，则△ABC与△DEF的周长比为________.2．(知识点2，3)如果两个相似三角形面积之比为19∶，那么它们对应边的比为________，对应角平分线的比为_______，周长之比为________.【解析】相似三角形对应边的比，对应角平分线的比，对应周长的比都等于相似比；面积的比等于相似比的平方．12∶13∶13∶13∶3．如图4－5－19所示，△ABC中，DE∥BC，AD∶DB＝12∶，则下列结论中正确的是()图4－5－19A.DEBC＝12B.DEBC＝13C.△ADE的周长△ABC的周长＝12D.S△ADES△ABC＝13B4．(知识点2)已知△ABC∽△A1B1C1，且S△ABCS△A1B1C1＝169，若AB＝2，则A1B1＝______.1.5【解析】△ABC∽△A1B1C1，S△ABCS△A1B1C1＝169＝ABA1B12，∴ABA1B1＝43，A1B1＝34×2＝1.5.图4－5－241.如图4－5－24，△ABD中，EF∥BD交AB于点E，交AD于点F，AC交EF于点G，交BD于点C，S△AEG＝18S四边形EBCG，则AGAC的值为()DA.34B.23C.12D.13BACDE如图，已知DE//BC,AB=30m,BD=18m,ΔABC的周长为80m，面积为100m2,求ΔADE的周长和面积30m18m1.顺次连结三角形各边中点所得小三角形与原三角形的周长之比为()A．12∶B．14∶C．21∶D．41∶2．如图所示，在▱ABCD中，如果M为CD的中点，AM与BD相交于点N，那么S△DMN：S△ABN为()A图4－5－21图4－5－20例2如图4－5－20所示，△ABC中，点D，E，F分别在边AB，AC，BC上，DE∥BC，EF∥AB，AEEC＝23，S△ABC＝S，求S▱BFED.2．如图4－5－25所示，有一块三角形土地，它的底边BC＝100m，高AH＝80m，某单位要沿着底边BC修一座底面是矩形DEFG的大楼．D，G分别在边AB，AC上，若大楼的宽DE是40m，求这个矩形的面积．【解析】运用相似三角形的性质，求出矩形的长．图4－5－25巩固提高如图，△ABC是一块锐角三角形余料，边BC=120毫米，高AD=80毫米，要把它加工成正方形零件，使正方形的一边在BC上，其余两个顶点分别在AB、AC上，这个正方形零件的边长是多少？NMQPEDCBA解：设正方形PQMN是符合要求的△ABC的高AD与PN相交于点E。设正方形PQMN的边长为x毫米。因为PNBC∥，所以△APNABC∽△所以AEAD=PNBC因此，得x=48（毫米）。答：-------。80–x80=x12012080x3．如图4－5－26，在△ABC中，∠C＝90°，AC＝30，AB＝50，a，b，c，…是△ABC内部的矩形，它们的一个顶点在AB上，一组对边分别在AC上或与AC平行，另一组对边分别在BC上或与BC平行，若各矩形在AC上的边长相等，矩形a的一边长为32，则这样的矩形a，b，c，…的个数是()图4－5－26AA．4B．5C．6D．7【解析】如图，EF∥BC，∴∠B＝∠GEF，∴∠BED＝∠EGF(等角的余角相等)；在Rt△BDE和Rt△EFG中，∠BED＝∠EGF，DE＝FG，∠BDE＝∠EFG＝90°，∴△BDE≌△EFG.同理，△EFG≌△GKH≌△HLM，∴BD＝EF＝GK＝HL＝BC－DC＝502－302...