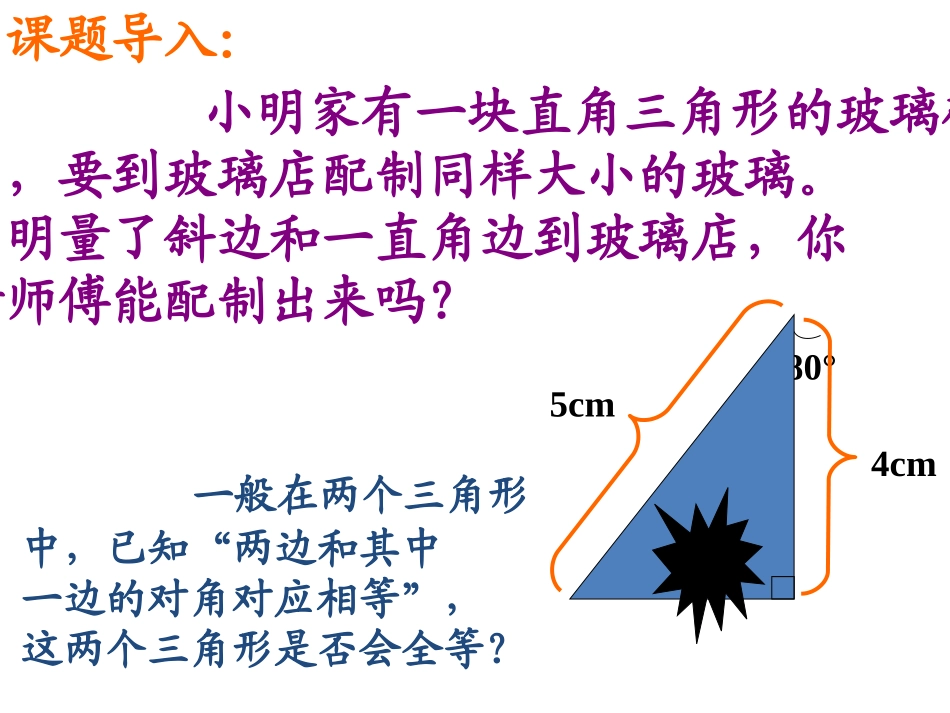
课题导入:小明家有一块直角三角形的玻璃破了,要到玻璃店配制同样大小的玻璃。小明量了斜边和一直角边到玻璃店,你猜师傅能配制出来吗?5cm80°4cm一般在两个三角形中,已知“两边和其中一边的对角对应相等”,这两个三角形是否会全等?(HL)复习旧知:大家知道:两边和其中一边的对角分别相等的两个三角形不一定全等。不能有:“边边角”或“SSA”ABCDEFE′新知探究:任意画一个RtAB△C,使∠C=90°.再画一Rt△A'B'C',使∠C'=90°,B'C'=BC,A'B'=AB,把画好RtA△'B'C'剪下来,放到RtABC△上,它们全等吗?归纳定理:两个直角三角形全等的判定:斜边和一条直角边分别相等的两个直角三角形全等。(可以简写成:“斜边、直角边”或“HL”)ABCA'B'C'巩固练习:1.小明家有一块直角三角形的玻璃破了,要到玻璃店配制同样大小的玻璃。小明量了斜边和一直角边到玻璃店,你猜师傅能配出来吗?5cm80°4cm2.如图,已知在RtABC△与Rt△A'B'C'中∠C=C∠'=90°,AC=A'C',BC=B'C',则RtABC△与RtA△'B'C'全等的根据是()AHLBASACSASDSSAABCA'B'C'3.如图,ACBC⊥,BDAD⊥,AC=BD.求证:BC=AD.ABCD小结2、隐含条件的找法1、直角三角形全等判定:3、直角三角形全等判定的应用:通过证明直角三角形全等,从而证明相关的边相等或角相等公共边或部分共边HL,SSS,SAS,ASA(AAS)1.如图,C是路段AB的中点,两人从C点同时出发,以相同的速度沿两条直线行走,并同时到达D、E两地。DA⊥AB,EB⊥AB,D、E与路段AB的距离相等吗?为什么?变式训练:ABDCE2.如图,已知AB=CD,AE⊥BC,DF⊥BC,CE=BF.求证:AE=DF.DABCFE3.如图,∠ABD=∠ACD=90°,BD=CD,AD与BC相交于点E.求证:BE=CE.ABCDE4.已知:如图,点P在线段AB上,ACAB⊥于A,DBAB⊥于B,PC=PD,AC=PB.求证:PCPD.⊥PACDB