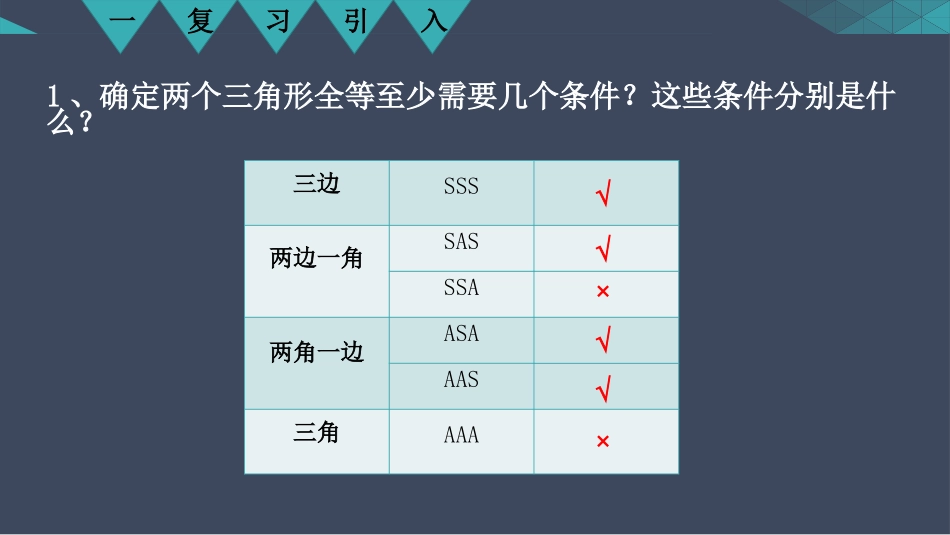
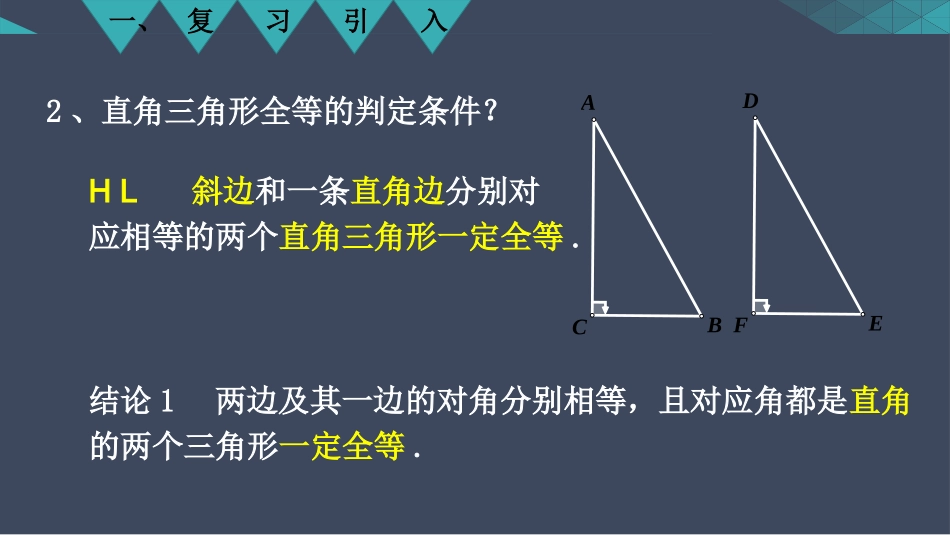
三角形全等的条件———SSA探究一复习引入1、确定两个三角形全等至少需要几个条件?这些条件分别是什么?三边SSS两边一角SASSSA两角一边ASAAAS三角AAA√√√√××一、复习引入2、直角三角形全等的判定条件?CBEFADHL结论1两边及其一边的对角分别相等,且对应角都是直角的两个三角形一定全等.斜边和一条直角边分别对应相等的两个直角三角形一定全等.二、动手操作1、对SSA中的角进行分类讨论②SSA中的对应角是锐角③SSA中的对应角是钝角①SSA中的对应角是直角2、已知△ABC满足∠B=30°,AB=9cm,AC=5cm,试画出满足条件的三角形,并说出满足条件的三角形的个数.二、动手操作3、改变△ABC中∠B、AB、AC的值,按照新给定的数值画出相应的三角形,并说出满足条件的三角形的个数?(分组合作,每个小组展示两个不同类型的作图)AC=5.00厘米AB=9.00厘米B=30.00°CC'AB三、归纳猜想4、根据所有作图结果进行分类讨论,并归纳得出猜想BCA123两边及其一边的对角分别对应相等,且对应角都是钝角的两个三角形一定全等.两边及其一边的对角分别对应相等,且对应角都是锐角的两个三角形不一定全等;两边及其一边的对角分别对应相等,且对应角都是直角的两个三角形一定全等;四、证明猜想如图,在钝角△ABC和△DEF中,∠B和∠E为钝角,且∠B=E∠,AB=DE,AC=DF.求证:△ABC≌DEF△ABCDEFHGBCAAC≥AB或AC=h当时,SSA不一定全等h五、深入探究h