三角形的重要线段VIP免费

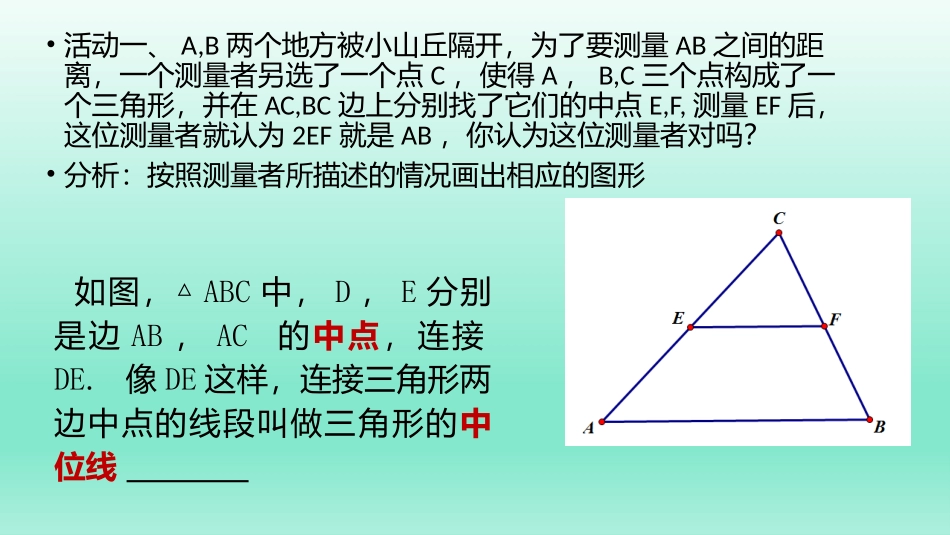
18.1.3三角形的中位线初二2班•活动一、A,B两个地方被小山丘隔开，为了要测量AB之间的距离，一个测量者另选了一个点C，使得A，B,C三个点构成了一个三角形，并在AC,BC边上分别找了它们的中点E,F,测量EF后，这位测量者就认为2EF就是AB，你认为这位测量者对吗？•分析：按照测量者所描述的情况画出相应的图形•活动一、A,B两个地方被小山丘隔开，为了要测量AB之间的距离，一个测量者另选了一个点C，使得A，B,C三个点构成了一个三角形，并在AC,BC边上分别找了它们的中点E,F,测量EF后，这位测量者就认为2EF就是AB，你认为这位测量者对吗？•分析：按照测量者所描述的情况画出相应的图形如图，△ABC中，D，E分别是边AB，AC的中点，连接DE.像DE这样，连接三角形两边中点的线段叫做三角形的中位线•猜想：看一看，量一量，猜一猜：•EF与AB之间有什么位置关系和数量关系？猜想：EF=1/2AB,EF//AB对猜想进行验证•结论：三角形中位线定理•三角形的中位线平行于三角形的第三边，并且等于第三边的一半几何语言的表示：练一练•(1)ABC△中,D、E分别是AB、AC的中点，BC=10cm，则DE=______.•(2)ABC△中,D、E分别是AB、AC的中点，∠A=50°,B=70°,∠则∠AED=_____三、例题讲解•如图，点D,E,F分别是AB,AC,BC边上的中点，请判断四边形CEDF的形状？并说明理由。解：四、巩固练习•1.如图，DE是△ABC的中位线，若BC=10，则DE的长为（）•A.4B.5C.6D.7•2.如图，在△ABC中，∠C=90°，D,E分别是AB，AC上的中点，AC=3，AB=5.求线段DE的长.•3如图，在四边形ABCD中，E,F,G,H分别为AB,BC,CD,DA的中点，四边形EFGH是平行四边形吗？为什么？五、课堂小结：•1要区分中位线和中线•2三角形的中位线定理是三角形一个重要的性质定理。包括两个方面（1）平行关系（2）线段的倍分关系。•3利用三角形的中位线定理推理得到一些重要的结论，顺次连接四边形的各边中点得到的新四边形也是平行四边形。