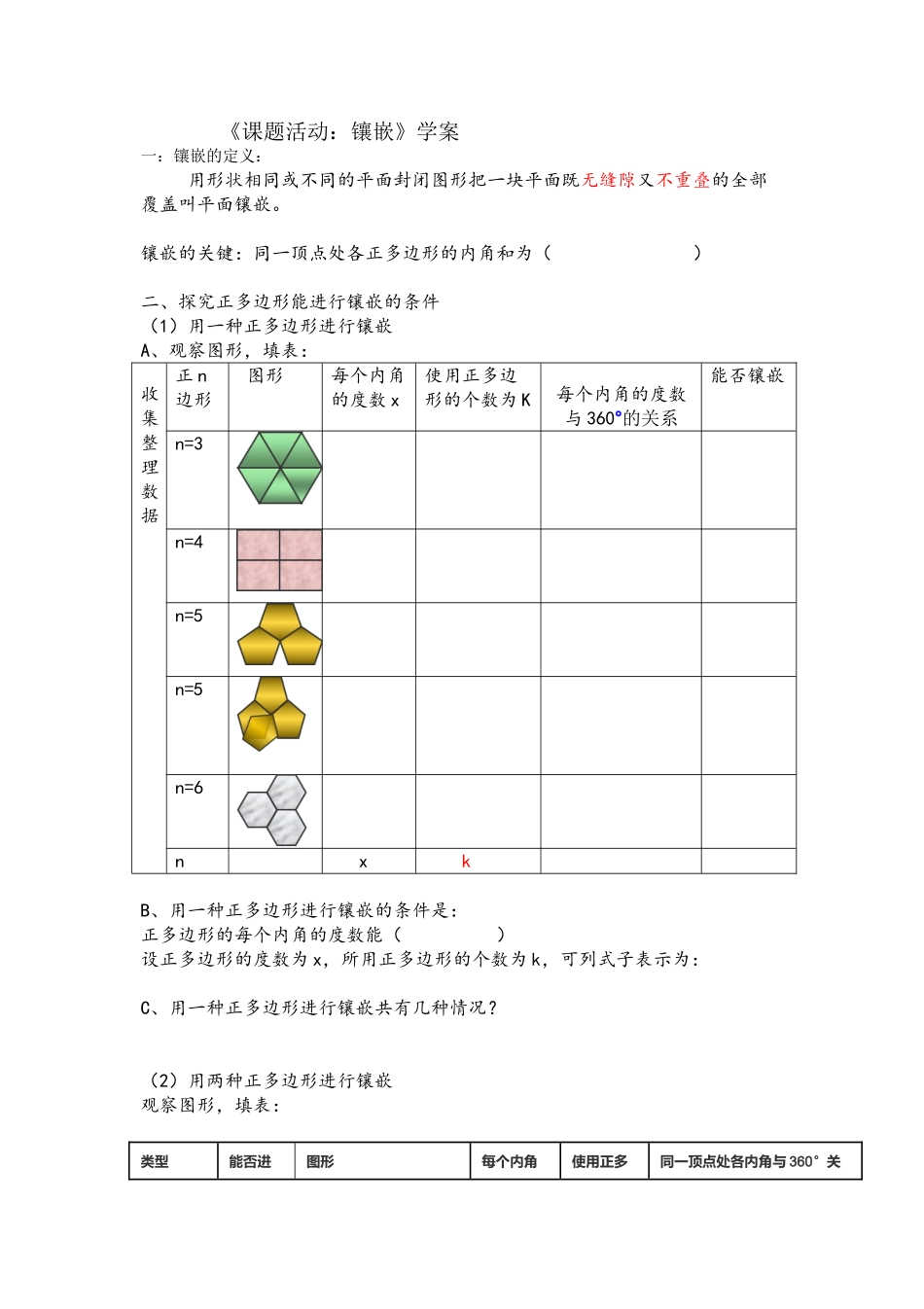
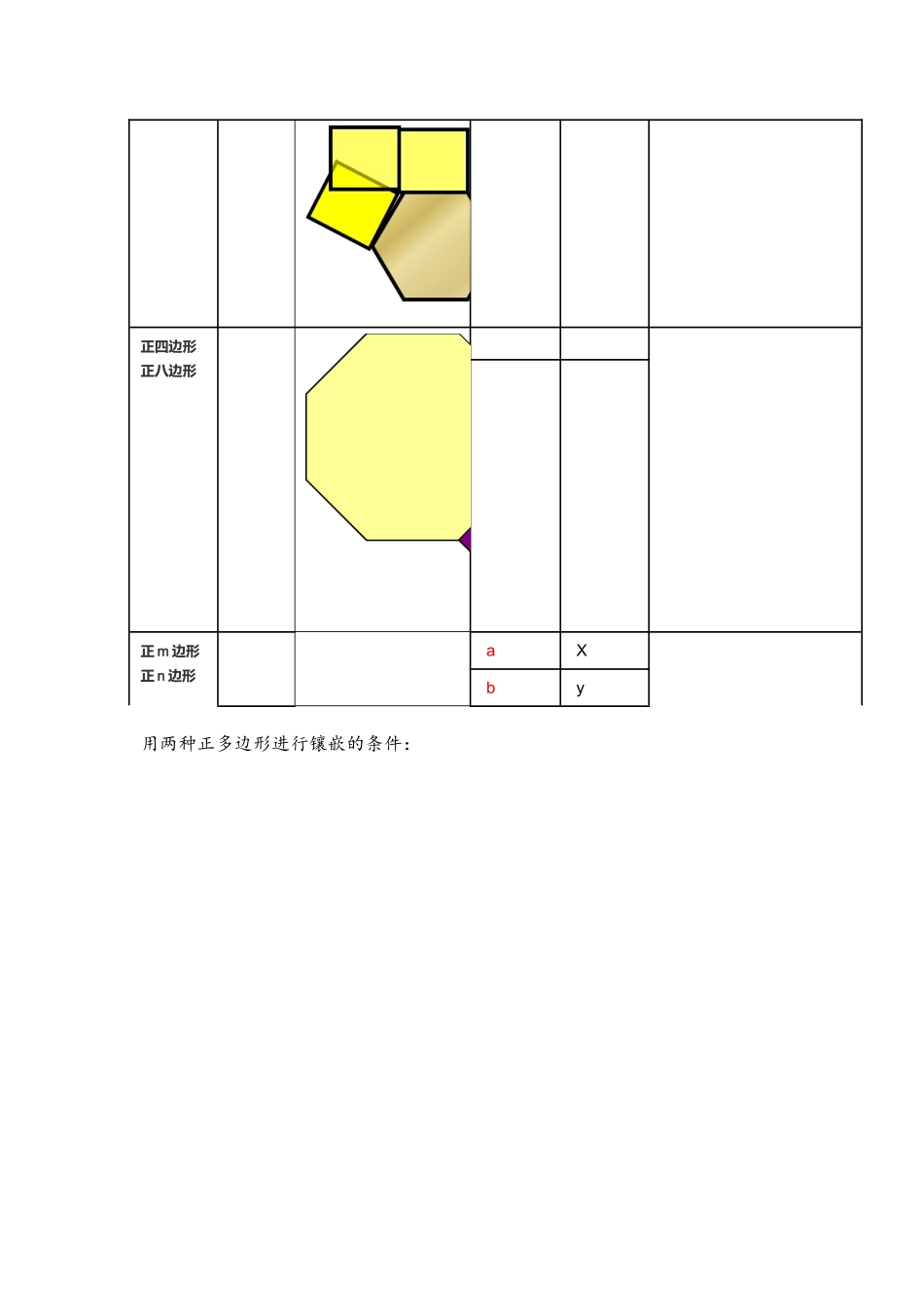
《课题活动:镶嵌》学案一:镶嵌的定义:用形状相同或不同的平面封闭图形把一块平面既无缝隙又不重叠的全部覆盖叫平面镶嵌。镶嵌的关键:同一顶点处各正多边形的内角和为()二、探究正多边形能进行镶嵌的条件(1)用一种正多边形进行镶嵌A、观察图形,填表:收集整理数据正n边形图形每个内角的度数x使用正多边形的个数为K每个内角的度数与360°的关系能否镶嵌n=3n=4n=5n=5n=6nxkB、用一种正多边形进行镶嵌的条件是:正多边形的每个内角的度数能()设正多边形的度数为x,所用正多边形的个数为k,可列式子表示为:C、用一种正多边形进行镶嵌共有几种情况?(2)用两种正多边形进行镶嵌观察图形,填表:类型能否进图形每个内角使用正多同一顶点处各内角与360°关行镶嵌度数边形的个数系正三角形正四边形3×60°+2×90°=360°正三角形正六边形正四边形正六边形正四边形正八边形正m边形正n边形aXby用两种正多边形进行镶嵌的条件: