1.1回归分析的基本思想及其初步应用-(2)VIP免费

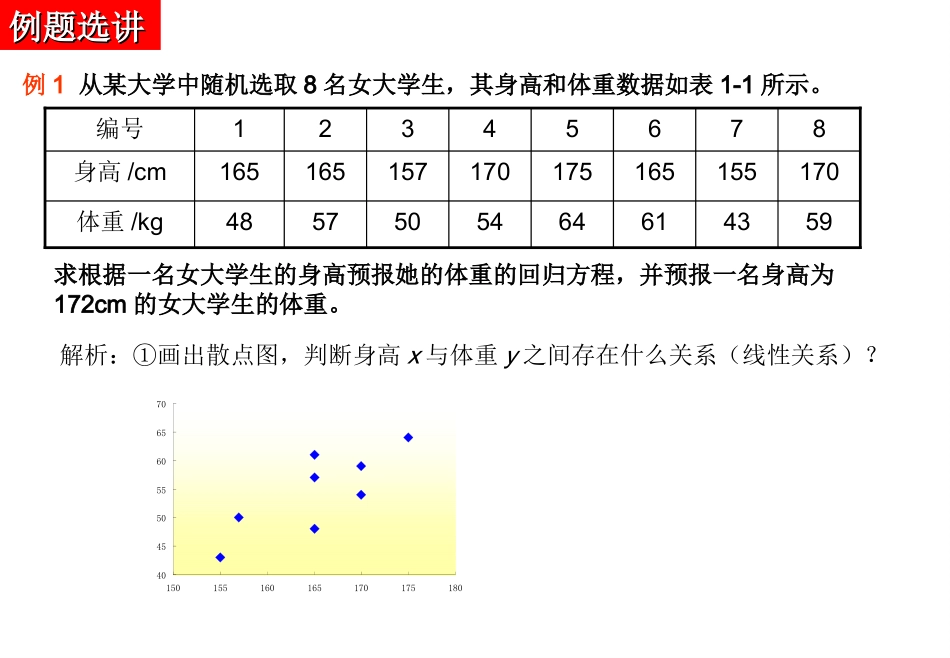
创设情景创设情景问题一：一般情况下，体重与身高有一定的关系，通常个子较高的人体重比较大，但这是否一定正确？（是否存在普遍性）问题二：统计方法解决问题的基本过程是什么？回归分析的基本过程：⑴画出两个变量的散点图；⑵判断是否线性相关⑶求回归直线方程（利用最小二乘法）⑷并用回归直线方程进行预报例1从某大学中随机选取8名女大学生，其身高和体重数据如表1-1所示。5943616454505748体重/kg170155165175170157165165身高/cm87654321编号求根据一名女大学生的身高预报她的体重的回归方程，并预报一名身高为172cm的女大学生的体重。例题选讲例题选讲解析：①画出散点图，判断身高x与体重y之间存在什么关系（线性关系）？40455055606570150155160165170175180②列表求出相关的量，并求出线性回归方程848.025.16582187745.5425.165872315ˆ22121xnxyxnyxbniiniii712.8525.165849.05.54ˆxbya代入公式有所以回归方程为712.85849.0ˆˆˆxxbay③利用回归方程预报身高172cm的女大学生的体重约为多少？kgy316.60712.85172849.0ˆ172x当时，求线性回归方程的步骤：第一步：作散点图—→第二步：求回归方程—→第三步：代值计算探究新知探究新知问题一:身高为172cm的女大学生的体重一定是60.316kg吗？（不一定，但一般可以认为她的体重在60.316kg左右.）由于所有的样本点不共线，而只是散布在某一直线的附近，所以身高和体重的关系可以用线性回归模型来表示：eabxy其中a和b为模型的未知参数，e称为随机误差.思考思考11：函数模型与“回归模型”的关系的不：函数模型与“回归模型”的关系的不同同函数模型：因变量y完全由自变量x确定回归模型：预报变量y完全由解释变量x和随机误差e确定因此，一次函数模型是线性回归模型的特殊形式，线性回归模型是一次函数模型的一般形式.(1)所用确定性函数不恰当；(2)忽略了某些因素的影响；(3)观测误差。思考2:产生随机误差项e的原因是什么？在线性回归模型中，R2表示解析变量对预报变量变化的贡献率。RR22越接近越接近11，表示回归的效果越好，表示回归的效果越好（因为R2越接近1，表示解析变量和预报变量的线性相关性越强）。如果某组数据可能采取几种不同回归方程进行回归分析，则可以通过比较R2的值来做出选择，即选取R2较大的模型作为这组数据的模型。注：相关系数R2是度量模型拟合效果的一种指标。在线性模型中，它代表自变量刻画预报变量的能力。问题二：如何衡量两个变量之间线性相关关系的强弱呢？22121()1()niiiniiyyRyy相关系数：1354总计0.36128.361残差变量0.64225.639回归变量比例平方和来源从上中可以看出，解析变量对总效应约贡献了从上中可以看出，解析变量对总效应约贡献了64%64%，，即即RR220.640.64，可以叙述为“身高解析了，可以叙述为“身高解析了64%64%的体重变化”，而的体重变化”，而随随机误差贡献了剩余的机误差贡献了剩余的36%36%。。所以，体重与身高有很强的线性相关性，从而表明我们所以，体重与身高有很强的线性相关性，从而表明我们建立的回归模型是有意义的建立的回归模型是有意义的；问题三：例1中由体重与身高建立的线性相关关系有无意义？巩固练习巩固练习1.假设关于某设备的使用年限x和支出的维修费用y（万元），有如下表的统计资料。试求：⑴画出数据的散点图；⑵若x与y呈线性相关关系，求线性回归方程y＝bx+a的回归系数a、b；⑶估计使用年限为10年时，维修费用是多少？⑴散点图如图：01234567802468xiyi⑵；；；23.1103.1245905453.112ˆ2b08.0423.15ˆˆxbya⑶回归直线方程是08.023.1ˆxy，10x38.1208.01023.1y当时，（万元）即估计使用10年时维修费用是12.38万元。小结小结1.熟练掌握求线性回归方程的步骤；2.理解线性回归模型与一次函数的不同；3.了解相关系数的计算与解释。