4.4.1参数方程的意义VIP免费

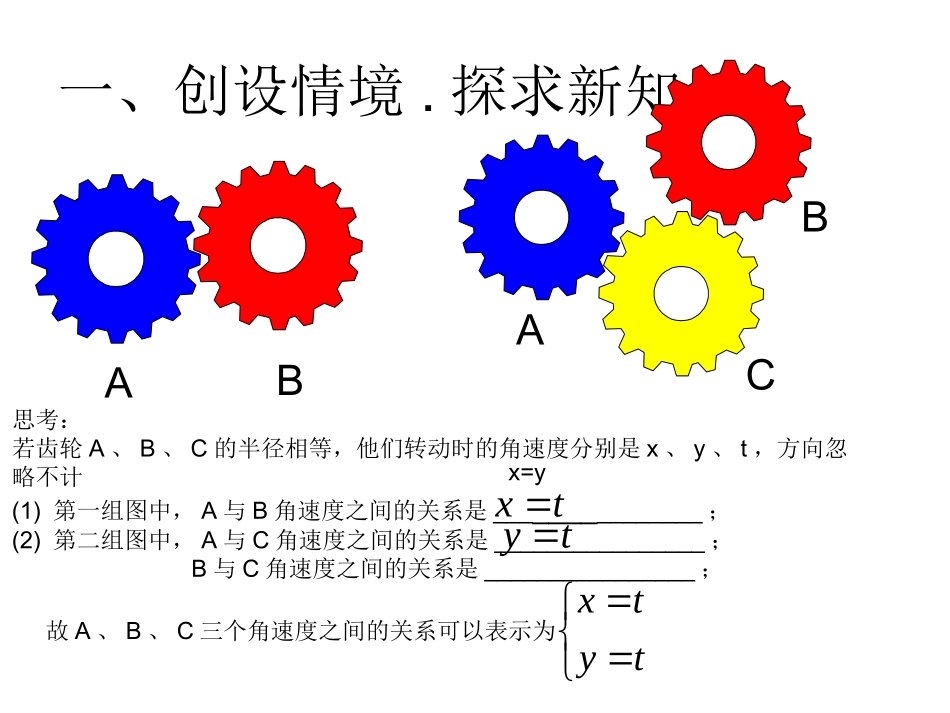
数学选修4-4参数方程的意义一、创设情境探求新知ABBAC一、创设情境.探求新知ABBAC思考：若齿轮A、B、C的半径相等，他们转动时的角速度分别是x、y、t，方向忽略不计(1)第一组图中，A与B角速度之间的关系是_______________；(2)第二组图中，A与C角速度之间的关系是________________；B与C角速度之间的关系是________________；x=ytytx故A、B、C三个角速度之间的关系可以表示为txty一、创设情境.探求新知ABBAC思考：若齿轮A、B、C的半径分别为4、1、2，他们转动时的角速度分别是x、y、t，方向忽略不计(1)第一组图中，它们角速度之间的关系是_________________；(2)第二组图中，它们角速度之间的关系是_________________；tytx221xy4二、建构概念.突破难点xyxytxy4tytx221方程方程213451234542016128246810201612841.填写下列两个表格，思考方程和方程的区别与联系2.满足方程的点(x,y)所形成的图形是什么呢？方程表示的是一条直线例1.如图，设圆的圆心在坐标原点，半径为1►求出该圆的标准方程二、建构概念.突破难点yxMM0O•••-1-11►试一试：能不能找出一个变量，“连接”圆上点的横坐标x和纵坐标y,进而得出圆的方程的不同表现形式?化建设限代步骤：标准方程：122yxθHy=sinθx=cosθsincosyx方程：（t是中间量）二、建构概念.突破难点tytx221sincosyx(θ是中间量，))20[，概括归纳：一般的，在平面直角坐标系中，如果曲线上任意一点的坐标x,y都是某个变数t的函数并且对于t的每一个允许值，由方程组所确定的点M(x,y)都在这条曲线上，那么方程就叫做这条曲线的参数方程，联系变数x,y的变数t叫做参变数，简称参数.()()()xfttDygt二、建构概念.突破难点概括归纳：相对于参数方程而言，直接给出点的坐标间关系的方程叫做普通方程.参数是联系变数x,y的桥梁，可以是一个有物理意义或几何意义的变数，也可以是没有明显实际意义的变数.思考:下列两个方程，是参数方程吗？二、建构概念.突破难点xyyx414tytx221例2.已知曲线C的参数方程是(t为参数)(1)判断点M1(0,1)，M2(5,4)与曲线C的位置关系三、巩固概念.理解应用1232tytx(2)已知点M3(6,a)在曲线C上，求a的值解：(1)把点M1的坐标(0,1)代入方程组，解得t=0，因此M1在曲线C上把点M2的坐标(5,4)代入方程组，得到，这个方程组无解，因此点M2不在曲线C上124352tt解：(2)因为点M3(6,a)在曲线C上，所以，解得t=2,a=9因此，a=912362tat1.曲线(t为参数)与x轴的焦点坐标是()A.(1,4)B.(,0)C.(1,-3)D.(,0)2.方程()所表示的曲线上一点是()A.(2,7)B.(,)C.(,)D.(1,0)三、巩固概念.理解应用3412tytx16251625cossinyx)2,0[31322121BD跟踪练习三、巩固概念.理解应用如图所示，已知点A(1，2)，B(5，6)，点M是线段AB上的一个动点，试求点M(x,y)轨迹的参数方程ABxyOABxy•MC解：设|MA|=t,易知,4BAC12214costtxM22224sinttyMtM点的轨迹方程是222122tytx)240t（跟踪练习三、巩固概念.理解应用如图所示，已知点A(1，2)，B(5，6)，点M是线段AB上的一个动点，试求点M(x,y)轨迹的参数方程ABxyC4BMH方案二：解：设|MB|=t,易知,ttxM2254cos5ttyM2264sin6M点的轨迹方程是tytx226225)240t（OABxy•MHt例1.如图，设圆的圆心在坐标原点，半径为1►求出该圆的普通方程yxMM0O•••-1-11►试一试：能不能找出一个变量，“连接”圆上点的横坐标x和纵坐标y,进而得出圆的参数方程?化建设限代步骤：普通方程：122yxθHy=sinθx=cosθsincosyx参数方程：►还能不能找出类似的变量？弧长、面积、周长三、巩固概念.理解应用例1.如图，设圆O的圆心在坐标原点，半径为1yxMM0O•••-1-11θHy=sinθx=cosθsincosyx参数方程：三、巩固概念.理解应用sincosyx)(R])20[(，思考：这两个参数方程都表示圆C吗？1、知识内容：知道圆的参数方程以及曲线参数方程的概念；能选取适当的参数建立参数方程；通过对圆和直线的参数方程的研究，理解其中参数的意义。2、思想与方法：参数思想。四、课堂小结.提升能力谢谢！