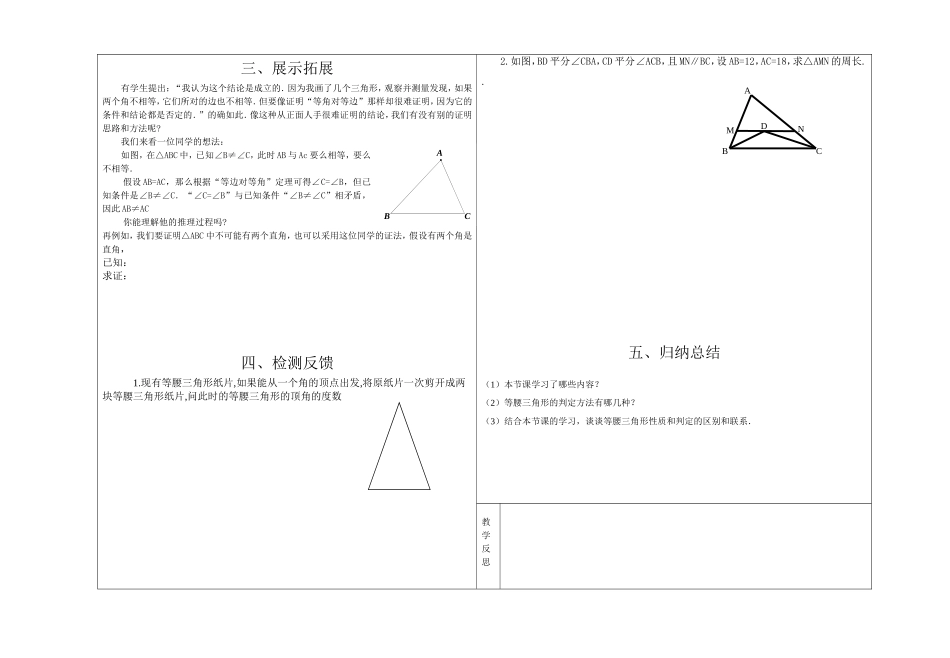
白银市三中导学案学科:数学年级:八主备人:高莉教研组长:吴正锋教务处:许承荣上课时间:2015年3月4日学生姓名:课题1.1.3等腰三角形课时4课型导学二、合作交流前面已经证明了等腰三角形的两个底角相等。反过来,有两个角相等的三角形是等腰三角形吗?1、如图:在△ABC中,∠B=∠C,求证:AB=AC.等腰三角形的判定方法:如果有一个三角形有两个角相等,那么这两个角所对的边,简写成。2如图,在△ABC中,BD平分∠ABC,交AC于点D,过D做DE∥BC,交AB于点E,请判断△BDE的形状,并说明理由。学习目标1.探索等腰三角形判定定理.2.理解等腰三角形的判定定理,并会运用其进行简单的证明.3.了解反证法的基本证明思路,并能简单应用。重难点重点:探索等腰三角形判定定理难点:理解等腰三角形的判定定理。一、自主预习学前准备:回想一下,我们探索过的等腰三角形的性质?性质1:;性质2:.2.如图,点D在AC上,点E在AB上,且AB=AC,BC=BD=BE,AE=DE,求∠A的度数。EDCBA三、展示拓展有学生提出:“我认为这个结论是成立的.因为我画了几个三角形,观察并测量发现,如果两个角不相等,它们所对的边也不相等.但要像证明“等角对等边”那样却很难证明,因为它的条件和结论都是否定的.”的确如此.像这种从正面人手很难证明的结论,我们有没有别的证明思路和方法呢?我们来看一位同学的想法:如图,在△ABC中,已知∠B≠∠C,此时AB与Ac要么相等,要么不相等.假设AB=AC,那么根据“等边对等角”定理可得∠C=∠B,但已知条件是∠B≠∠C.“∠C=∠B”与已知条件“∠B≠∠C”相矛盾,因此AB≠AC你能理解他的推理过程吗?再例如,我们要证明△ABC中不可能有两个直角,也可以采用这位同学的证法,假设有两个角是直角,已知:求证:四、检测反馈1.现有等腰三角形纸片,如果能从一个角的顶点出发,将原纸片一次剪开成两块等腰三角形纸片,问此时的等腰三角形的顶角的度数2.如图,BD平分∠CBA,CD平分∠ACB,且MN∥BC,设AB=12,AC=18,求△AMN的周长..五、归纳总结(1)本节课学习了哪些内容?(2)等腰三角形的判定方法有哪几种?(3)结合本节课的学习,谈谈等腰三角形性质和判定的区别和联系.教学反思CBANMCBAD