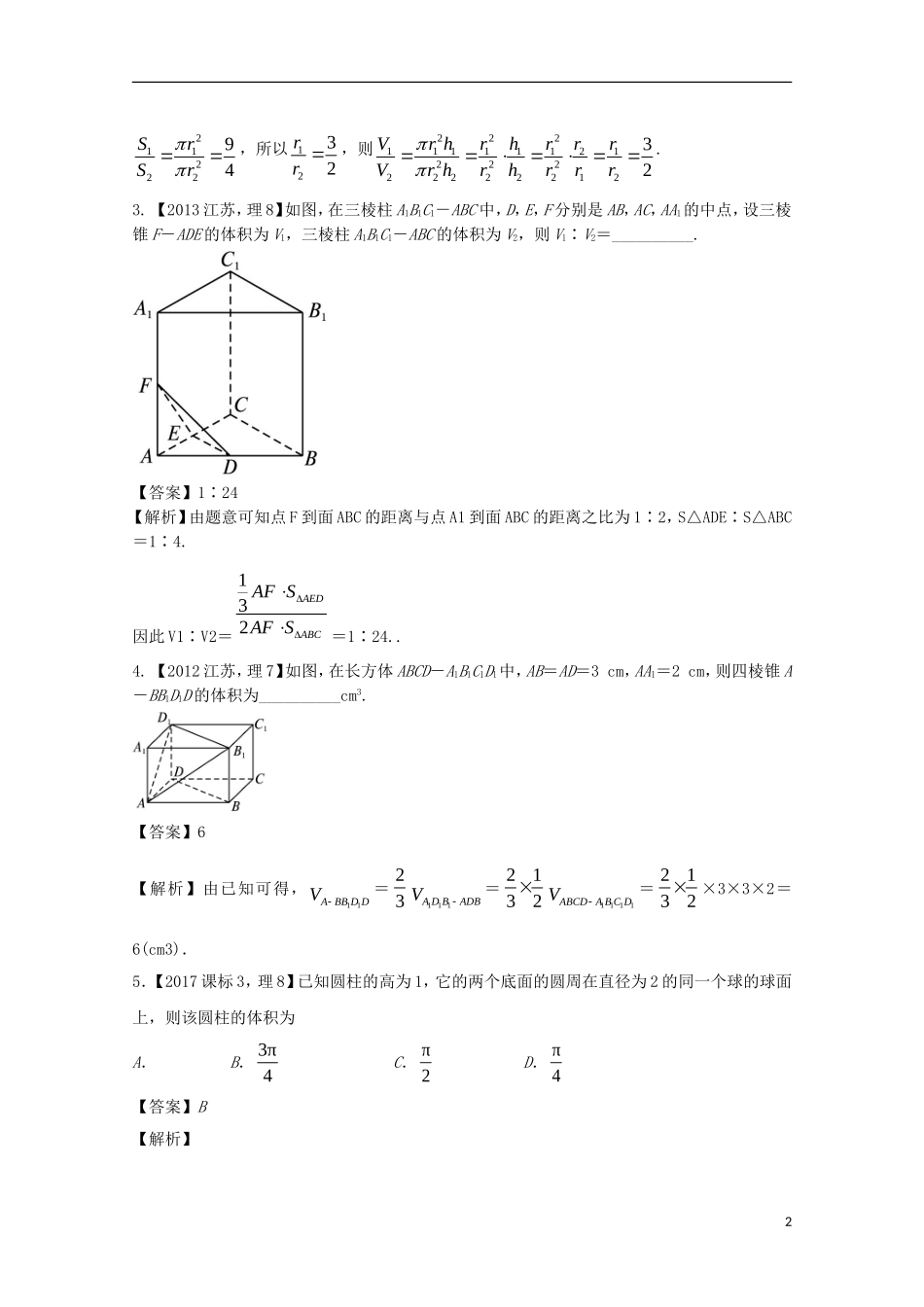
专题1空间几何体【三年高考】1.【2017江苏】如图,在圆柱12OO内有一个球O,该球与圆柱的上、下底面及母线均相切.记圆柱12OO的体积为1V,球O的体积为2V,则12VV的值是▲.【答案】32【解析】设球半径为,则213223423VrrVr.故答案为32.【考点】圆柱的体积、球的体积【名师点睛】空间几何体体积问题的常见类型及解题策略:①若给定的几何体是可直接用公式求解的柱体、锥体或台体,则可直接利用公式进行求解;②若所给定的几何体的体积不能直接利用公式得出,则常用转换法、分割法、补形法等方法进行求解.2.【2014江苏,理8】设甲,乙两个圆柱的底面面积分别为12,SS,体积为12,VV,若它们的侧面积相等且1294SS,则12VV的值是.【答案】32【解析】设甲、乙两个圆柱的底面和高分别为11rh、,22rh、,则112222rhrh,1221hrhr,又121122294SrSr,所以1232rr,则222111111212222222221232VrhrhrrrVrhrhrrr.3.【2013江苏,理8】如图,在三棱柱A1B1C1-ABC中,D,E,F分别是AB,AC,AA1的中点,设三棱锥F-ADE的体积为V1,三棱柱A1B1C1-ABC的体积为V2,则V1∶V2=__________.【答案】1∶24【解析】由题意可知点F到面ABC的距离与点A1到面ABC的距离之比为1∶2,S△ADE∶S△ABC=1∶4.因此V1∶V2=132AEDABCAFSAFS=1∶24..4.【2012江苏,理7】如图,在长方体ABCD-A1B1C1D1中,AB=AD=3cm,AA1=2cm,则四棱锥A-BB1D1D的体积为__________cm3.【答案】6【解析】由已知可得,11ABBDDV=23111ADBADBV=21321111ABCDABCDV=2132×3×3×2=6(cm3).5.【2017课标3,理8】已知圆柱的高为1,它的两个底面的圆周在直径为2的同一个球的球面上,则该圆柱的体积为A.B.3π4C.π2D.π4【答案】B【解析】2【考点】圆柱的体积公式【名师点睛】(1)求解以空间几何体的体积的关键是确定几何体的元素以及线面的位置关系和数量关系,利用相应体积公式求解;(2)若所给几何体的体积不能直接利用公式得出,则常用等积法、分割法、补形法等方法进行求解.6.【2017天津,理10】已知一个正方体的所有顶点在一个球面上,若这个正方体的表面积为18,则这个球的体积为.【答案】92【解析】设正方体边长为,则226183aa,外接球直径为344279233,πππ3382RaVR.【考点】球【名师点睛】求多面体的外接球的面积和体积问题常用方法有(1)三条棱两两互相垂直时,可恢复为长方体,利用长方体的体对角线为外接球的直径,求出球的半径;(2)直棱柱的外接球可利用棱柱的上下底面平行,借助球的对称性,球心为上下底面外接圆的圆心连线的中点,再根据3勾股定理求球的半径;(3)如果设计几何体有两个面相交,可过两个面的外心分别作两个面的垂线,垂线的交点为几何体的球心,本题就是第三种方法.7.【2017课标1,理16】如图,圆形纸片的圆心为O,半径为5cm,该纸片上的等边三角形ABC的中心为O.D、E、F为圆O上的点,△DBC,△ECA,△FAB分别是以BC,CA,AB为底边的等腰三角形.沿虚线剪开后,分别以BC,CA,AB为折痕折起△DBC,△ECA,△FAB,使得D、E、F重合,得到三棱锥.当△ABC的边长变化时,所得三棱锥体积(单位:cm3)的最大值为_______.【答案】415【解析】4【考点】简单几何体的体积【名师点睛】对于三棱锥最值问题,肯定需要用到函数的思想进行解决,本题解决的关键是设好未知量,利用图形特征表示出三棱锥体积.当体积中的变量最高次是2次时可以利用二次函数的性质进行解决,当变量是高次时需要用到求导得方式进行解决.8.【2016高考新课标3理数改编】在封闭的直三棱柱111ABCABC内有一个体积为V的球,若ABBC,6AB,8BC,13AA,则V的最大值是.【答案】92【解析】试题分析:要使球的体积V最大,必须球的半径R最大.由题意知球的与直三棱柱的上下底面都相切时,球的半径取得最大值32,此时球的体积为334439()3322R.考点:1、三棱柱的内切球;2、球的体积.【思维拓展】立体几何是的最值问题通常有三种思考方向:(1)根据几何体的结构特征,变动态为静态,直观判断在什么情况下取得最值;(2)将几何体...