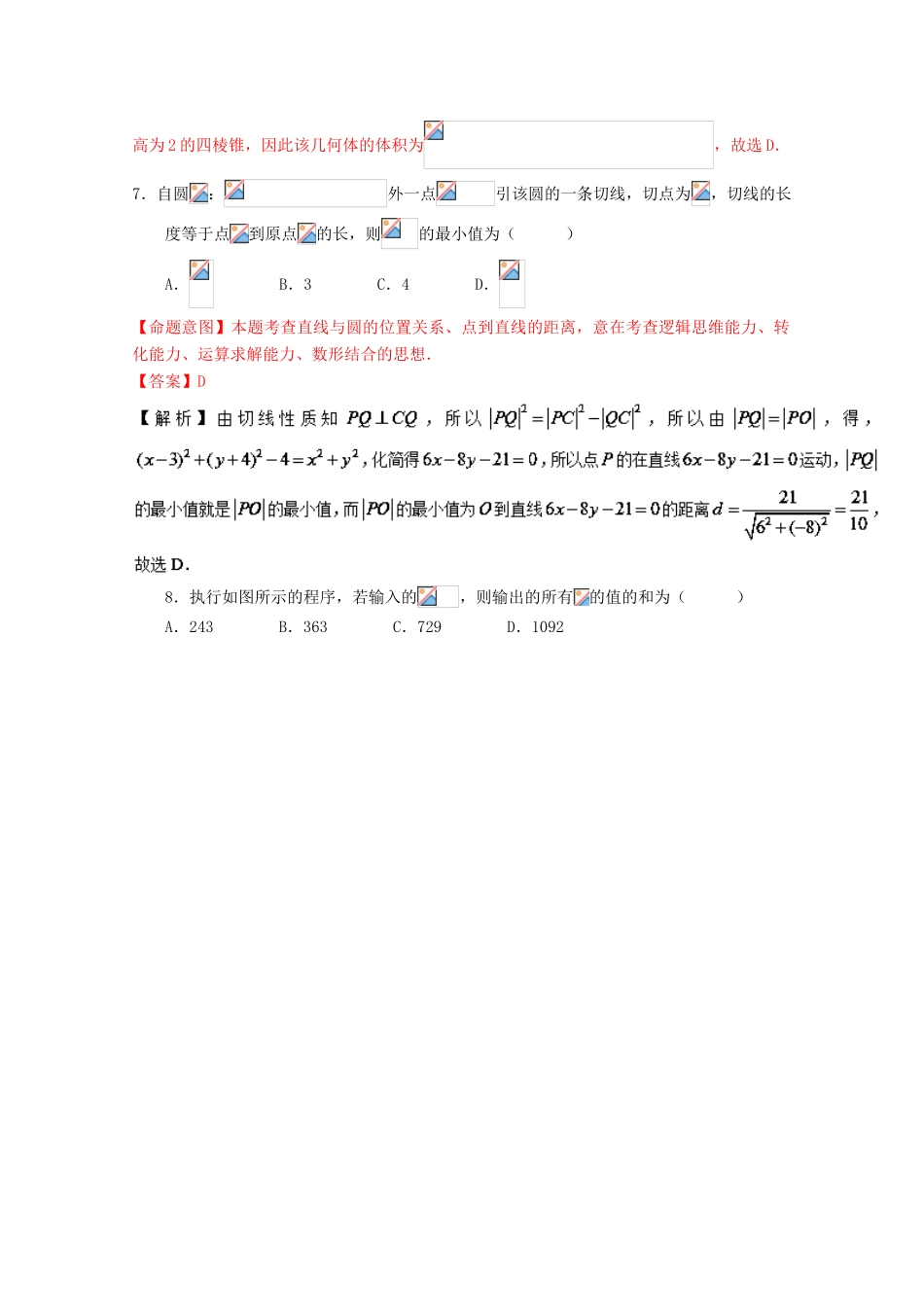
(新课标Ⅰ卷)2016年高考数学押题预测卷理全卷满分150分考试时间120分钟第Ⅰ卷(共60分)一、选择题(本大题共12个小题,每小题5分,共60分.在每小题给出的四个选项中,只有一项是符合题目要求的.)1.已知集合,,则()A.B.C.D.【命题意图】本题考查集合的交集运算,意在考查计算能力.【答案】C【解析】当时,,所以,故选C.2.若复数在复平面内对应的点关于轴对称,且,则复数在复平面内对应的点在()A.第一象限B.第二象限C.第三象限D.第四象限【命题意图】本题考查复数的几何意义、模与代数运算等基础知识,意在考查转化思想与计算能力.【答案】D3.已知函数,若,则()A.2B.1C.-1D.-2【命题意图】本题考查分段函数的求值,意在考查分类讨论思想与计算能力.【答案】B【解析】因为,所以,故选B.4.某市重点中学奥数培训班共有14人,分为两个小组,在一次阶段考试中两个小组成绩的茎叶图如图所示,其中甲组学生成绩的平均数是88,乙组学生成绩的中位数是89,则的值是()A.10B.11C.12D.13【命题意图】本题考查样本平均数、中位数、茎叶图等基础知识,意在考查识图能力和计算能力.【答案】C【解析】由题意,得甲组中,解得.乙组中,所以,所以,故选C.5.已知向量若,则()A.B.C.2D.【命题意图】本题考查平面向量的坐标运算、数量积与模等基础知识,意在考查转化思想、方程思想、逻辑思维能力与计算能力.【答案】A6.某几何体的三视图如图所示,则该几何体的体积为()A.B.C.D.【命题意图】本题考查三视图、圆柱与棱锥的体积计算,意在考查识图能力、转化能力、空间想象能力.【答案】D【解析】由三视图知几何体为一个底面半径为2高为4的半圆柱中挖去一个以轴截面为底面高为2的四棱锥,因此该几何体的体积为,故选D.7.自圆:外一点引该圆的一条切线,切点为,切线的长度等于点到原点的长,则的最小值为()A.B.3C.4D.【命题意图】本题考查直线与圆的位置关系、点到直线的距离,意在考查逻辑思维能力、转化能力、运算求解能力、数形结合的思想.【答案】D8.执行如图所示的程序,若输入的,则输出的所有的值的和为()A.243B.363C.729D.1092【命题意图】本题考查程序框图的识别和运算,意在考查识图能力、简单的计算能力.【答案】D【解析】当时,是整数;当时,是整数;依次类推可知当时,是整数,则由,得,所以输出的所有的值为3,9,27,81,243,729,其和为1092,故选D.9.已知函数的一条对称轴方程为,则函数的最大值为()A.1B.±1C.D.【命题意图】本题考查三角变换、三角函数的对称性与最值,意在考查逻辑思维能力、运算求解能力、转化思想与方程思想.【答案】A10.四棱锥的底面为正方形,底面,,若该四棱锥的所有顶点都在体积为同一球面上,则()A.3B.C.D.【命题意图】本题考查空间直线与平面间的垂直和平行关系、球的体积,意在考查空间想象能力、逻辑推理能力、方程思想、运算求解能力.【答案】B【解析】连结交于点,取的中点,连结,则,所以底面,则到四棱锥的所有顶点的距离相等,即球心,均为,所以由球的体积可得,解得,故选B.11.已知过双曲线的右焦点的直线交双曲线于两点,连结,若,且,则双曲线的离心率为()A.B.C.D.【命题意图】本题考查双曲线定义与几何性质,意要考查逻辑思维能力、运算求解能力,以及考查数形结合思想、方程思想、转化思想.【答案】B12.已知函数,其中,为自然对数的底数.当时,函数的图象不在直线的下方,则实数的取值范围()A.B.C.D.【命题意图】本题考查函数图象与性质、利用导数研究函数的单调性、零点存在性定理,意在考查逻辑思维能力、等价转化能力、运算求解能力,以及构造思想、分类讨论思想的应用.【答案】B【解析】由题意设,且在时恒成立,而.令,则,所以在上递增,所以.当时,,在上递增,,符合题意;当时,,在上递减,,与题意不合;当时,为一个递增函数,而,,由零点存在性定理,必存在一个零点,使得,当时,,从而在上单调递减,从而,与题意不合,综上所述:的取值范围为,故选B.第Ⅱ卷(共90分)二、填空题(每题5分,满...