4.5相似三角形的性质及应用-(2)VIP免费

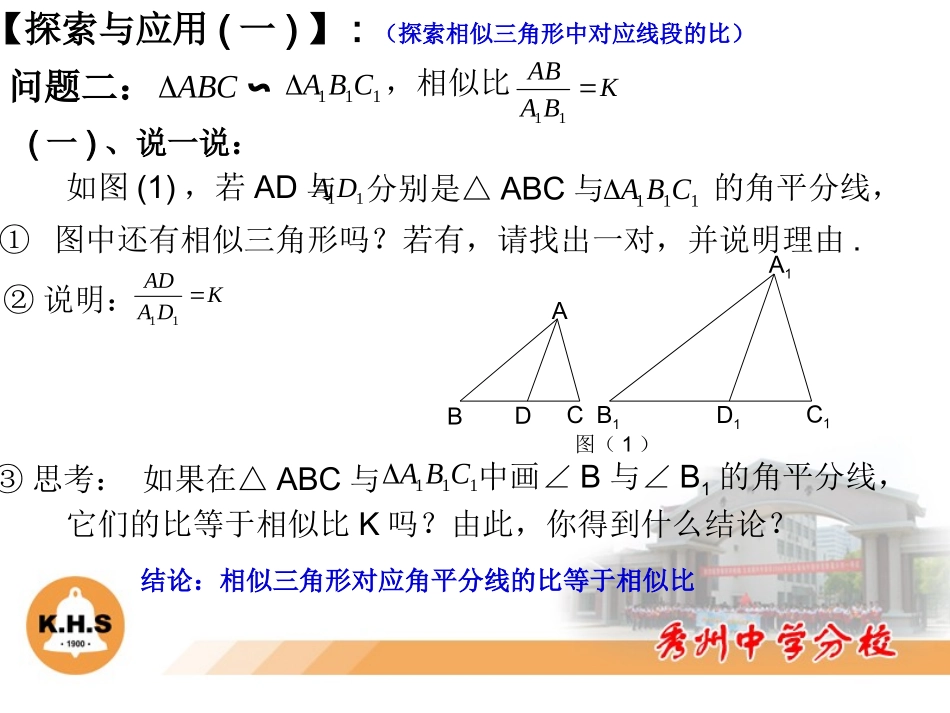
4.5相似三角形的性质及其应用(1)【知识回顾】:（相似三角形的性质）问题一：在4倍的放大镜下看到的三角形与原三角形相比，三角形的角、边是否都被放大了4倍？为什么？答：角保持不变，边放大了4倍。因为：相似三角形对应角相等，对应边成比例。【探索与应用(一)】:（探索相似三角形中对应线段的比）问题二：ABC∽111CBA，相似比KBAAB11①图中还有相似三角形吗？若有，请找出一对，并说明理由.如图(1)，若AD与11DA分别是△ABC与111CBA的角平分线，②说明：KDAAD11③思考：如果在△ABC与111CBA中画∠B与∠B1的角平分线，它们的比等于相似比K吗？由此，你得到什么结论？ABDCA1B1C1D1图（1）结论：相似三角形对应角平分线的比等于相似比(一)、说一说：【探索与应用(一)】:（探索相似三角形中对应线段的比）问题二：ABC∽111CBA，相似比KBAAB11在图(2)、图(3)中，你还能画出哪些对应线段，使它们的比等于相似比K。A1B1C1ABC图（2）A1B1C1ABC图（3）图(2)中画的是：.图(3)中画的是：.①请画一画，并把相关信息填在下面的横线上,然后尝试说明理由.理由：理由：②由此，你得到什么结论？相似三角形对应高线的比等于相似比相似三角形对应中线的比等于相似比（二）、画一画：【探索与应用(一)】:（探索相似三角形中对应线段的比）（三）、做一做：3131．②如图，ABC∽111CBA相似比4311BAABA1B1C1ABCDD1D，D1分别是AB,A1B1上的点，且AD=AB,A1D1=A1B1。11DCCD则．43①如图，D，E分别是AC，AB上的点，∠ADE＝∠B，AGBC⊥于点G，AFDE⊥于点F，若AD=３，AB=５，AFAG则AABCDEFG35ABDC图（４）【探索与应用(二)】:（探索三角形中线的性质）问题三：如图(４),BD是ABC的中线.(一)、说一说：图（４）中，你能根据中线的性质找到那些相等的量？（二）、画一画：ABC的中线CE,交BD于P,交AB于E.BPDP=CPEP②求的值.①说明BPDP1:2EP﹍﹍﹍①AD=CD②SABD△=SACD△重心(2)、在(1)中，如果把作(１)、在图(４)中,作出ABC的中线CE改成作中线AF,则与BD的交点还是点P吗?这又说明了什么？(3)、三角形三条中线的交点分每一条中线成两条线段，其中交点到中点与交点到顶点的距离之比为.（我们把三角形三条中线的交点叫做三角形的.）ABDCＦ21三角形三条中线相交于一点（三）、做一做：【探索与应用(二)】:（探索三角形中线的性质）如图，在△ABC中，中线AD,BE相交于点O，若SBOD△=5，则SAOB△=,SABC△=.ABCDEO１０３０•通过这堂课的经历，你探索到了哪些知识点？•感悟到了哪些思想与方法？【反思与感悟】:1、作业本（2）2、同步练习（课后提高题选做）【自主作业】: