探究与发现祖暅原理与柱体、椎体、球体的体积-(2)VIP免费

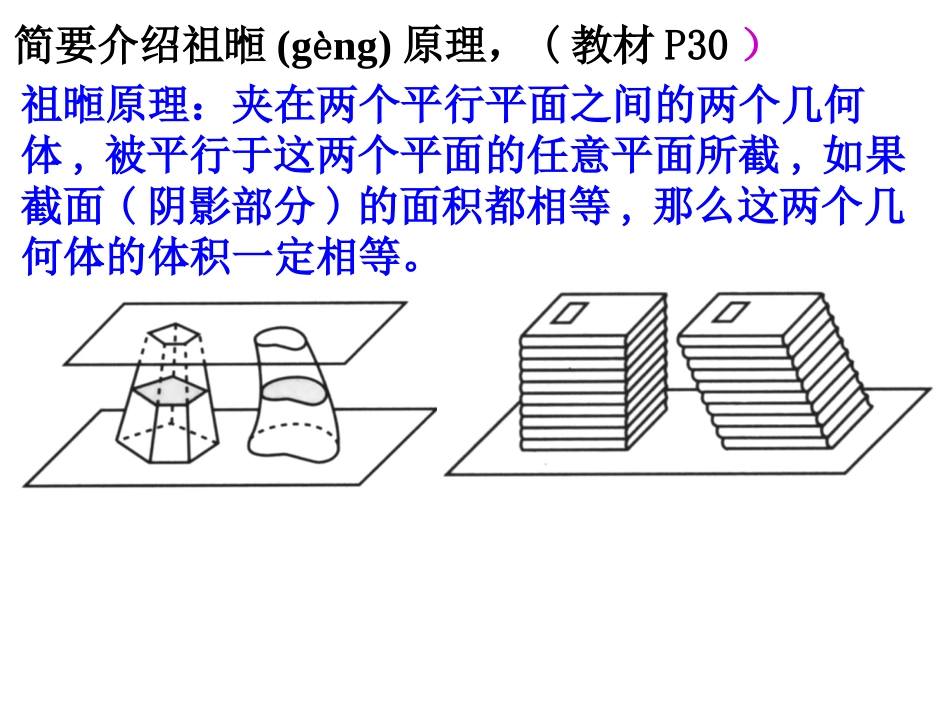
授课老师:陈国定祖暅原理与柱体、锥体、球体的体积必修二第一章探究与发现小实验：将一叠作业本放在桌面上组成一个几何体，将它改变一下形状，几何体的形状发生了改变，几何体的高发生改变了吗？几何体的体积发生改变了吗？说明理由！简要介绍祖暅(gèng)原理，(教材P30）祖暅原理：夹在两个平行平面之间的两个几何体,被平行于这两个平面的任意平面所截,如果截面(阴影部分)的面积都相等,那么这两个几何体的体积一定相等。祖暅是南北朝时代著名数学家祖冲之的儿子。受家庭的影响，尤其是父亲的影响，他从小热爱科学对数学具有浓厚的兴趣。祖冲之除了在计算圆周率方面的成就，还与他的儿子祖暅一起，用巧妙的方法解决了柱体，锥体，球体的体积计算。他们当时采用的原理，在西方被称为“卡瓦列利”原理，但这是在祖氏父子以后一千多年才由意大利数学家卡瓦列利发现的。为了纪念祖氏父子的这一伟大发现，数学上也称这个原理为“祖暅原理”。还有很多以姓名命名的公式或定理，比如呢？欧拉定理:简单多面体的顶点数V、面数F及棱数E间有关系V+F-E=2用秦九韶算法求当x=5时多项式f(x)=2x5–5x4–4x3+3x2–6x+7的值.解:首先将原多项式改写成如下形式:f(x)=((((2x-5)x-4)x+3)x-6)x+7hSV底长方体从而我们可以得到所有柱体的体积是___________hSV底柱体探究柱体的体积公式如图，下面是底面积都等于S，，高都等于h的任意棱柱，圆柱和长方体，你能用祖暅原理推导柱体的体积公式吗？如图，下面是底面积都等于S，高都等于h的任意棱锥和圆锥，你能用祖暅原理推导锥体的体积公式吗？如果三棱锥的底面积是S，高是h，那么它的体积是V三棱锥＝?ABCA1C1B1把三棱锥以△ABC为底面、AA1为侧棱补成一个三棱柱。探究锥体的体积公式问：一个（斜或正）三棱柱可以分割成几个三棱锥？ACA1BB1C1A1BB1C1AA1BC1ACBC1分成的每个锥体的体积有什么关系？说明理由。锥体的体积hSV底锥体31设球的半径为R,截面半径为r,平面与截面的距离为那么22lRrRrlo因此S圆=2r=()22lR=2R2loO1LPNKlBO2lS圆环=2R2l圆环面积S圆=S圆环根据祖日恒原理，这两个几何体的体积相等，即V球=312RRRR2=323R21所以V球=343R练习1:某几何体的三视图如图所示，则其体积为_____解析由三视图可知该几何体是如图所示的半个圆锥，底面半圆的半径r＝1，高SO＝2，则V几何体＝13×π×22＝π3.答案π3ABCPVPCPBPAPCPBPA，，求：两两垂直，，，已知在三棱锥中1练习2BACP三个全等的等腰直角三角形+正三角形的正三棱锥CAPB四个直角三角形？1,2,3PCPBPA若改为点P到平面ABC的距离呢？DBAC各面全为RT△BADC还有更特殊的吗正四面体DABCOOABCSO2017全国卷1小结1、一个重要的结论：祖暅原理等截面等高的两个几何体的体积相等2、几何体的体积公式：shv31锥体3、锥体球体体积公式推导过程所揭示的数学思想和方法：一个思想：“等价转换”一个方法：“割补法”V球=343R同学们，这节课有收获吗？shv柱体4、等体积法求点到面的距离