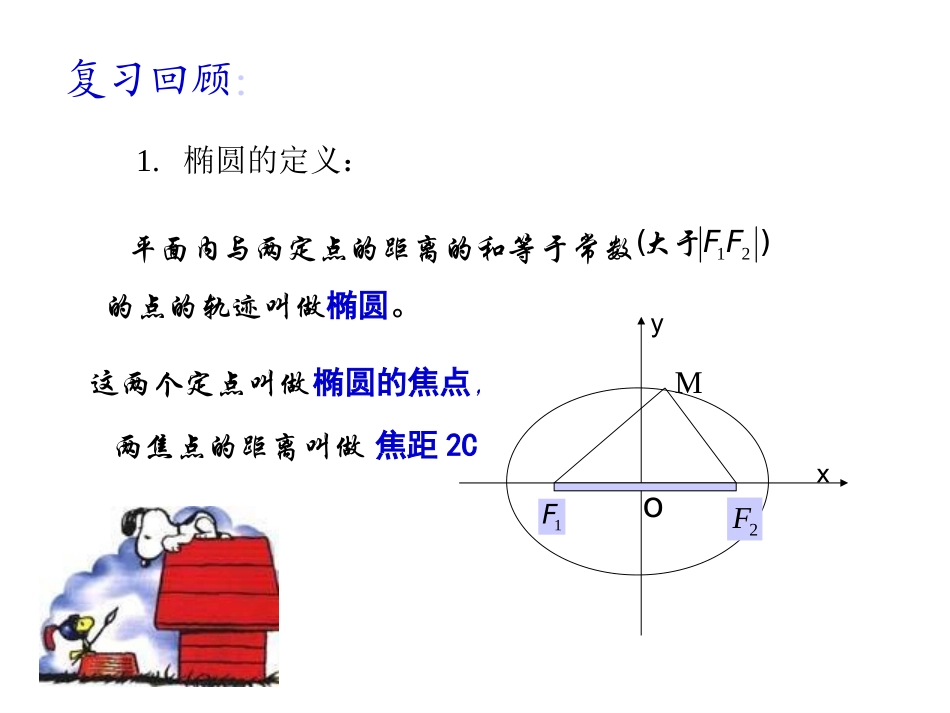
复习回顾:1.椭圆的定义:平面内与两定点的距离的和等于常数的点的轨迹叫做椭圆。)(21FF大于这两个定点叫做两焦点的距离叫做o1F2FxyM椭圆的焦点,焦距2C2.椭圆的标准方程:12222bxay12222byax(a>b>0)(a>b>0)或221mxny(不确定焦点在哪个轴上时)0mn一、椭圆的范围oxy由11122222222byaxbyax和即byax和X=aX=-ay=-by=b说明:椭圆位于直线X=±a和y=±b所围成的矩形之中。二、椭圆的对称性)0(12222babyax在坐标轴是椭圆的对称轴,原点是椭圆的对称中心中心:椭圆的对称中心叫做椭圆的中心oxy三、椭圆的顶点)0(12222babyax在中,令x=0,得y=?,说明椭圆与y轴的交点?令y=0,得x=?说明椭圆与x轴的交点?*顶点:椭圆与它的对称轴的四个交点,叫做椭圆的顶点。oxyB1(0,b)B2(0,-b)A1(-a,0)A2(a,0)︱︱F1F2*长轴、短轴:线段A1A2、B1B2分别叫做椭圆的长轴和短轴。a、b分别叫做椭圆的长半轴长和短半轴长。四、椭圆的离心率oxyace离心率:椭圆的焦距与长轴长的比:叫做椭圆的离心率。(1)离心率的取值范围:因为a>c>0,(2)离心率对椭圆形状的影响:1)e越接近1,c就越接近a,从而b就越小,2)e越接近0,c就越接近0,从而b就越大3)特例:e=0,则a=b,则c=0,两个焦点重合,椭圆方程变为(?)离心率的变化:0(小)1(大)椭圆的变化圆扁所以0b>0)上的一动点,当坐标为_____时到原点的最大距离为_____当的坐标为_____时到原点的最小距离为____,设F则当的坐标为_____时F的距离最大为__,的坐标为_____时F的距离最小为____。12(2,0),(4,0),(3)若椭圆经过(1,0),且焦点为FF则其离心率为_____(4)已知椭圆的一个焦点将长轴分成4:3两段,椭圆的离心率等于_____-12注意:数形结合在解题中的运用-17