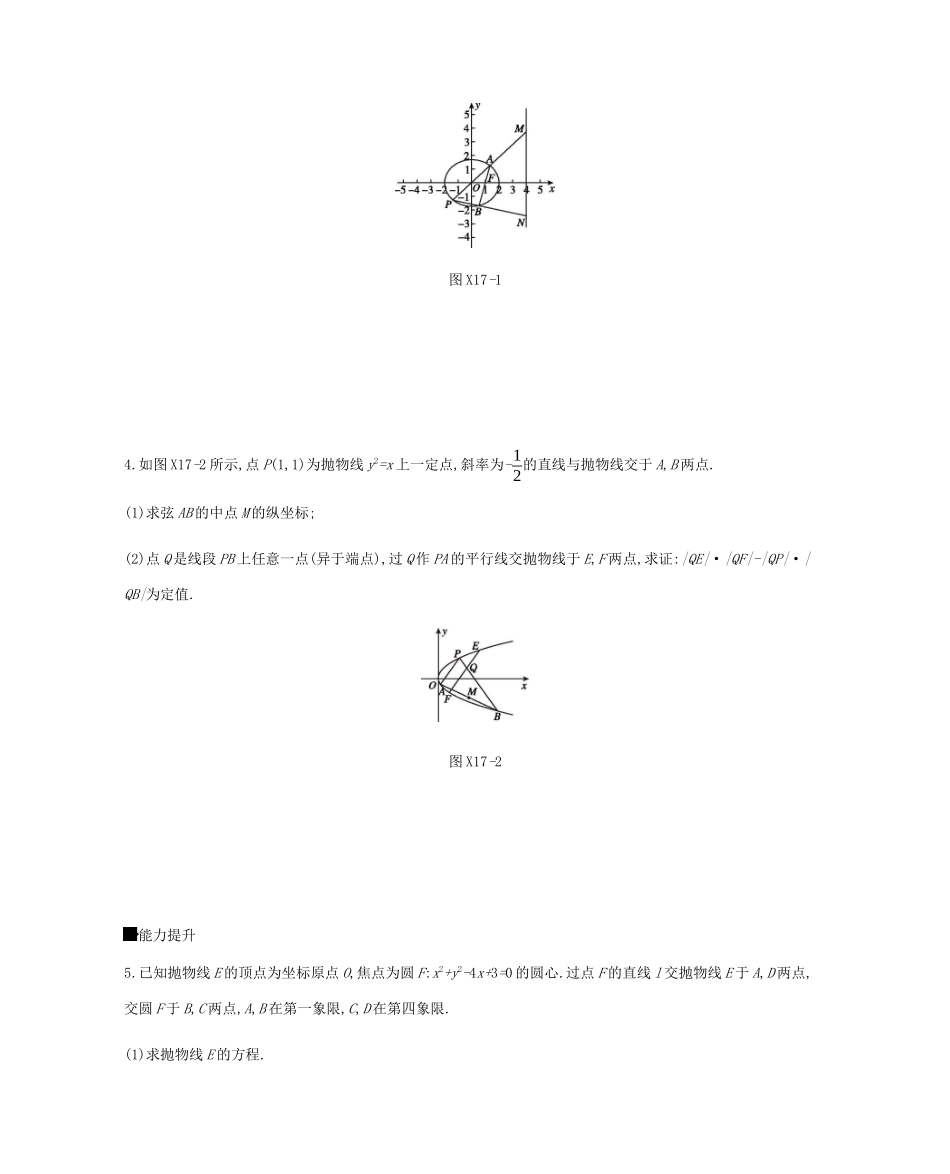
限时集训(十七)圆锥曲线中的定点、定值、存在性问题基础过关1.已知直线l与抛物线y2=2x交于A,B(异于坐标原点O)两点.(1)若直线l的方程为y=x-2,求证:OA⊥OB.(2)若OA⊥OB,则直线l是否恒过定点?若恒过定点,求出定点坐标;若不过定点,请说明理由.2.已知圆O:x2+y2=4,点F(1,0),P为平面内一动点,以线段FP为直径的圆内切于圆O,设动点P的轨迹为曲线C.(1)求曲线C的轨迹方程.(2)M,N是曲线C上的动点,且直线MN经过定点0,12,问在y轴上是否存在定点Q,使得∠MQO=∠NQO?若存在,请求出定点Q;若不存在,请说明理由.3.如图X17-1所示,已知椭圆Γ:x24+y23=1的右焦点为F,过点F且斜率为k的直线与椭圆Γ交于A(x1,y1),B(x2,y2)两点(点A在x轴上方),点A关于坐标原点的对称点为P,直线PA,PB分别交直线l:x=4于M,N两点,记M,N两点的纵坐标分别为yM,yN.(1)求直线PB的斜率(用k表示).(2)求点M,N的纵坐标yM,yN(用x1,y1表示),并判断yM·yN是否为定值.若是,请求出该定值;若不是,请说明理由.图X17-14.如图X17-2所示,点P(1,1)为抛物线y2=x上一定点,斜率为-12的直线与抛物线交于A,B两点.(1)求弦AB的中点M的纵坐标;(2)点Q是线段PB上任意一点(异于端点),过Q作PA的平行线交抛物线于E,F两点,求证:|QE|·|QF|-|QP|·|QB|为定值.图X17-2能力提升5.已知抛物线E的顶点为坐标原点O,焦点为圆F:x2+y2-4x+3=0的圆心.过点F的直线l交抛物线E于A,D两点,交圆F于B,C两点,A,B在第一象限,C,D在第四象限.(1)求抛物线E的方程.(2)是否存在直线l使得2|BC|是|AB|与|CD|的等差中项?若存在,求直线l的方程;若不存在,请说明理由.6.已知椭圆C:x2a2+y2b2=1(a>b>0)的左、右焦点分别为F1,F2,且离心率为12,点M为椭圆上一动点,△F1MF2面积的最大值为❑√3.(1)求椭圆C的标准方程.(2)设A,B分别为椭圆的左、右顶点,过点B作x轴的垂线l1,D为l1上异于点B的一点,以BD为直径作圆E.若过点F2的直线l2(异于x轴)与圆E相切于点H,且l2与直线AD相交于点P,试判断|PF1|+|PH|是否为定值,并说明理由.限时集训(十七)基础过关1.解:(1)证明:由{y=x-2,y2=2x,得x2-6x+4=0,解得x=3±❑√5,不妨取A(3-❑√5,1-❑√5),B(3+❑√5,1+❑√5),∴⃗OA·⃗OB=0,∴OA⊥OB.(2)显然直线l的斜率不为0,设直线l的方程为x=ty+m(m≠0),A(x1,y1),B(x2,y2),由{x=ty+m,y2=2x,消去x得y2-2ty-2m=0,∴y1y2=-2m,x1x2=y122·y222=m2,由OA⊥OB,得⃗OA·⃗OB=x1x2+y1y2=m2-2m=0,∴m=2,直线l的方程为x=ty+2,∴直线l恒过定点,且定点坐标为(2,0).2.解:(1)设PF的中点为S,切点为T,连接OS,ST,则|OS|+|SF|=|OT|=2,取F关于y轴的对称点F',连接F'P,故|F'P|+|FP|=2(|OS|+|SF|)=4>|FF'|=2.所以点P的轨迹是以F',F为焦点,长轴长为4的椭圆,设其方程为x2a2+y2b2=1(a>b>0),则a=2,c=1,b=❑√3,所以曲线C的方程为x24+y23=1.(2)假设存在满足题意的定点Q,设Q(0,m).当直线MN的斜率存在且不为0时,设直线MN的方程为y=kx+12(k≠0),M(x1,y1),N(x2,y2).由{x24+y23=1,y=kx+12,消去y,得(3+4k2)x2+4kx-11=0,则x1+x2=-4k3+4k2,x1·x2=-113+4k2.由∠MQO=∠NQO,得直线MQ与NQ的斜率之和为0,即y1-mx1+y2-mx2=kx1+12-mx1+kx2+12-mx2=2kx1x2+(12-m)(x1+x2)x1x2=0,即2kx1x2+(12-m)(x1+x2)=2k·-113+4k2+(12-m)·-4k3+4k2=4k(m-6)3+4k2=0,得m=6,所以存在定点Q(0,6)满足题意.当MN的斜率不存在或斜率为0时定点Q(0,6)也符合题意.综上,存在定点Q(0,6)满足题意.3.解:(1)由题,设直线AB的方程为y=k(x-1)(k≠0),由{y=k(x-1),x24+y23=1,消去y,得(4k2+3)x2-8k2x+4k2-12=0,则{x1+x2=8k24k2+3,x1x2=4k2-124k2+3,又P(-x1,-y1),所以kPB=y1+y2x1+x2=k(x1-1)+k(x2-1)x1+x2=-34k.(2)直线PA的方程为y=y1x1x,所以yM=4y1x1.由题意可知,k=y1x1-1,所以直线PB的方程为y+y1=-3¿¿(x+x1),则yN=-3¿¿-y1.因为x124+y123=1,所以yM·yN=-3¿¿-4y12x1=-3x12+4y12+9x1-12x1=-9,所以,yM·yN为定值-9.4.解:(1)设A(xA,yA),B(xB,yB),则yA2=xA,yB2=xB,两式相减得(yA-yB)(yA+yB)=xA-xB,所以kAB=yA-yBxA-xB=1yA+yB=-12,所以yA+yB=-2,所以弦AB的中点M的纵坐标yM=yA+yB2=-1.(2)证明:设Q(x0,y0),直线EF:x-x0=t1(y-y0),由{x-x0=t1(y-y0),y2=x,得y2-t1y+t1y0-x0=0,所以yE+yF=t1,yE·yF=t1y0-x0,|QE|·|QF|...