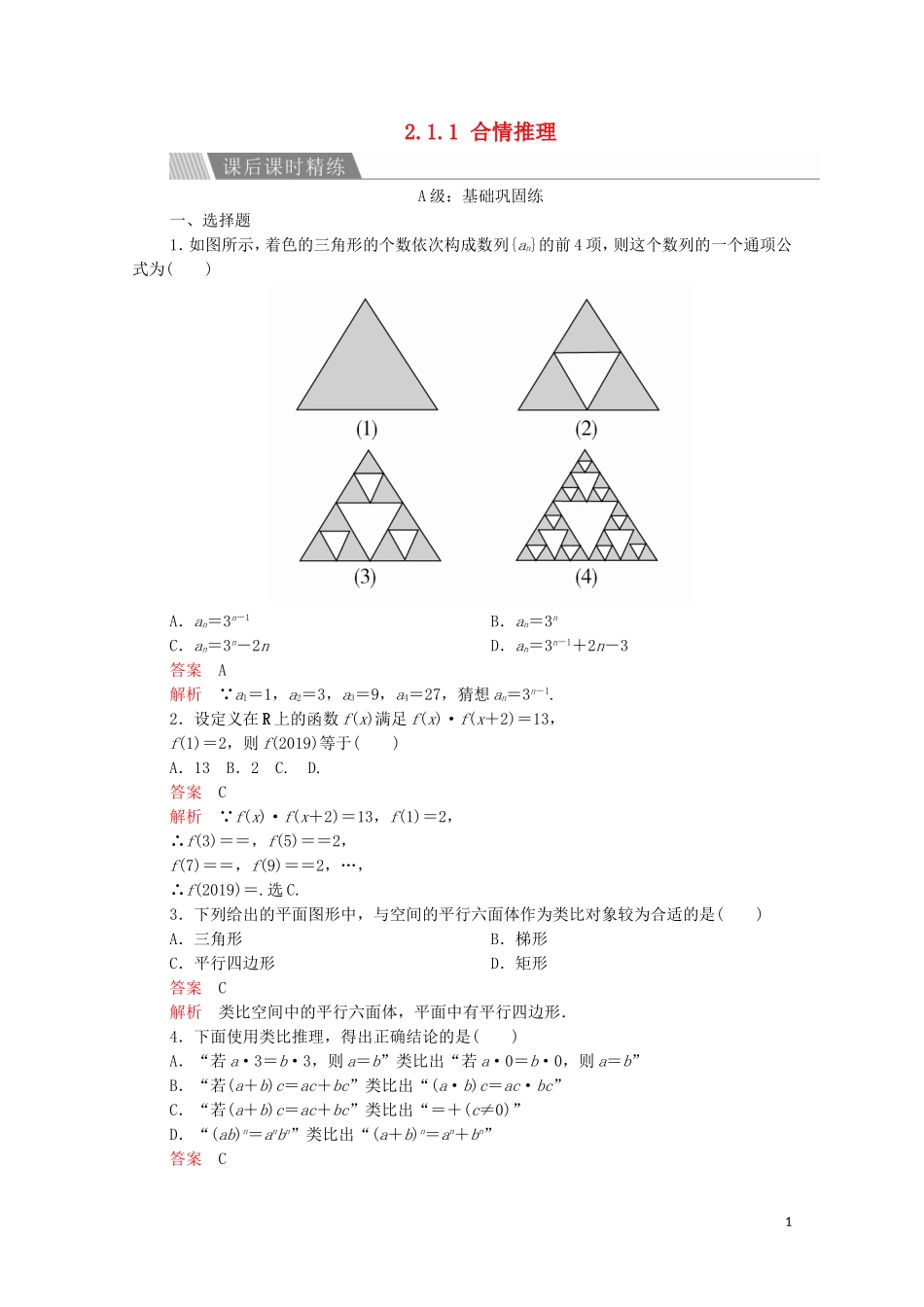
2.1.1合情推理A级:基础巩固练一、选择题1.如图所示,着色的三角形的个数依次构成数列{an}的前4项,则这个数列的一个通项公式为()A.an=3n-1B.an=3nC.an=3n-2nD.an=3n-1+2n-3答案A解析∵a1=1,a2=3,a3=9,a4=27,猜想an=3n-1.2.设定义在R上的函数f(x)满足f(x)·f(x+2)=13,f(1)=2,则f(2019)等于()A.13B.2C.D.答案C解析∵f(x)·f(x+2)=13,f(1)=2,∴f(3)==,f(5)==2,f(7)==,f(9)==2,…,∴f(2019)=.选C.3.下列给出的平面图形中,与空间的平行六面体作为类比对象较为合适的是()A.三角形B.梯形C.平行四边形D.矩形答案C解析类比空间中的平行六面体,平面中有平行四边形.4.下面使用类比推理,得出正确结论的是()A.“若a·3=b·3,则a=b”类比出“若a·0=b·0,则a=b”B.“若(a+b)c=ac+bc”类比出“(a·b)c=ac·bc”C.“若(a+b)c=ac+bc”类比出“=+(c≠0)”D.“(ab)n=anbn”类比出“(a+b)n=an+bn”答案C1解析A中,3与0两个数的性质不同,故类比中把3换成0,其结论不成立;B中,乘法满足对加法的分配律,但乘法不满足对乘法的分配律;C是正确的;D中,令n=2显然不成立.5.在平面直角坐标系内,方程+=1表示在x,y轴上的截距分别为a,b的直线,拓展到空间直角坐标系内,在x,y,z轴上的截距分别为a,b,c(abc≠0)的平面方程为()A.++=1B.++=1C.++=1D.ax+by+cz=1答案A解析因为在平面直角坐标系中,方程+=1表示的图形是一条直线,具有特定性质:“在x轴、y轴上的截距分别为a,b”,类比到空间直角坐标系中,在x,y,z轴上截距分别为a,b,c(abc≠0)的平面方程为++=1.6.在数学解题中,常会碰到形如“”的结构,这时可类比正切的和角公式.如:设a,b是非零实数,且满足=tan,则=()A.4B.C.2D.答案D解析将已知式变形,则有===tan,类比正切的和角公式,即tan(α+β)=,可知只有当=tan=时,上式成立.二、填空题7.经计算发现下列不等式:+<2,+<2,+<2,…根据以上不等式的规律,试写出一个对正实数a,b都成立的条件不等式:________.答案+<2(a>0,b>0且a≠b,a+b=20)解析观察题目所给的不等式,归纳可得出两根号下的两数之和为20.8.等差数列{an}中,an>0,公差d>0,则有a4·a6>a3·a7,类比上述性质,在等比数列{bn}中,若bn>0,q>1,写出b5,b7,b4,b8的一个不等关系:________.答案b4+b8>b5+b7解析在等差数列{an}中,an>0,公差d>0,∴{an}是各项均为正数的递增数列,∵4+6=3+7,且a4·a6>a3·a7,∴在等比数列{bn}中,bn>0,q>1,则{bn}为各项均为正数的递增数列.又∵4+8=5+7,∴b4+b8>b5+b7.9.观察下列等式:-2+-2=×1×2;-2+-2+-2+-2=×2×3;-2+-2+-2+…+-2=×3×4;-2+-2+-2+…+-2=×4×5;…照此规律,-2+-2+-2+…+-2=________.答案n(n+1)解析每组角的分母恰好等于右边两个相邻正整数因数的和,因此答案为n(n+1).三、解答题10.已知数列{an}的第一项a1=1,且an+1=(n=1,2,3,…).(1)求a2,a3,a4,a5;(2)归纳猜想这个数列的通项公式.2解(1)当n=1时,a1=1,由an+1=(n∈N*),得a2=,a3==,a4==,a5==.(2)由a1=1=,a2=,a3=,a4=,a5=,可归纳猜想an=(n∈N*).B级:能力提升练11.过△ABC边AB上任一点O分别作OA1∥AC,OB1∥BC,与BC,AC分别交于点A1,B1,则+为定值1.试写出类比到空间的结论.解如图1所示,这个命题的正确性很容易由相似三角形的性质推出,也不难用“面积法”证得定值为1,类比到空间,则有:如图2所示,过四面体VABC的面ABC上任一点O,分别作OA1∥VA,OB1∥VB,OC1∥VC,其中A1,B1,C1分别是所作直线与侧面的交点,则++为定值1.12.我们知道12=1,22=(1+1)2=12+2×1+1,32=(2+1)2=22+2×2+1,42=(3+1)2=32+2×3+1,…n2=(n-1)2+2(n-1)+1,左右两边分别相加,得n2=2×[1+2+3+…+(n-1)]+n,所以1+2+3+…+(n-1)=.类比上述推理方案写出求12+22+32+…+n2的表达式的过程.解记S1(n)=1+2+3+…+n,S2(n)=12+22+32+…+n2,Sk(n)=1k+2k+3k+…+nk(k∈N*).已知13=1,23=(1+1)3=13+3×12+3×1+1,33=(2+1)3=23+3×22+3×2+1,43=(3+1)3=33+3×32+3×3+1,…n3=(n-1)3+3(n-1)2+3(n-1)+1.将左右两边分别相加,得S3(n)=[S3(n)-n3]+3[S2(n)-n2]+3[S1(n)-n]+n.由此知S2(n)===.34