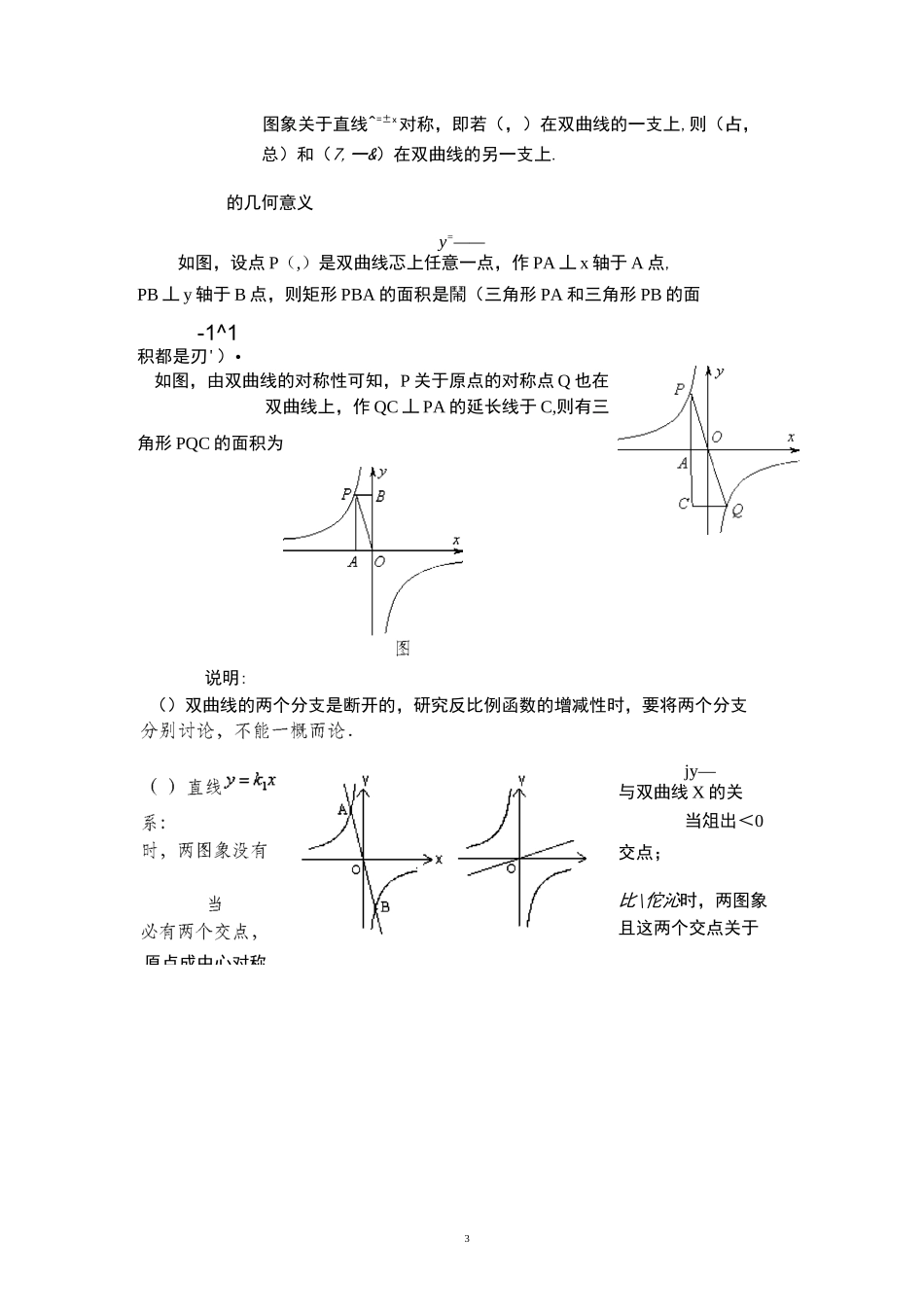
1反比例函数知识点归纳和典型例题知识点归纳(一)反比例函数的概念ky=—1-忑(疋HO)可以写成y=^-(疋HO)的形式,注意自变量的指数为-1,在解决有关自变量指数问题时应特别注意系数七工0这一限制条件;ky=—.忑(七HO)也可以写成的形式,用它可以迅速地求出反比例函数解析式中的,从而得到反比例函数的解析式;kV=—•反比例函数X的自变量疋H0,故函数图象与轴、轴无交点•(二)反比例函数的图象ky=—在用描点法画反比例函数疋的图象时,应注意自变量的取值不能为,且应对称取点(关于原点对称)•(三)反比例函数及其图象的性质hy=—•函数解析式:X(疋HO)•自变量的取值范围:忑工0•图象:()图象的形状:双曲线•阳越大,图象的弯曲度越小,曲线越平直•鬧越小,图象的弯曲度越大•()图象的位置和性质:与坐标轴没有交点,称两条坐标轴是双曲线的渐近线•当疋nO时,图象的两支分别位于一、三象限;在每个象限内,随的增大而减小;当疋co时,图象的两支分别位于二、四象限;在每个象限内,随的增大而增大•2()对称性:图象关于原点对称,即若(,)在双曲线的一支上,则(—住,一b)在双曲线的另一支上.3图象关于直线^=±x对称,即若(,)在双曲线的一支上,则(占,总)和(7,一&)在双曲线的另一支上.的几何意义y=——如图,设点P(,)是双曲线忑上任意一点,作PA丄x轴于A点,PB丄y轴于B点,则矩形PBA的面积是鬧(三角形PA和三角形PB的面-1^1积都是刃')•如图,由双曲线的对称性可知,P关于原点的对称点Q也在双曲线上,作QC丄PA的延长线于C,则有三角形PQC的面积为说明:()双曲线的两个分支是断开的,研究反比例函数的增减性时,要将两个分支jy—与双曲线X的关当俎出<0交点;比\佗沁时,两图象且这两个交点关于原点成中心对称.4()下列函数中,是的反比例函数的是()•y-3=2xy=^2()下列函数中,是的反比例函数的是()•(四)充分利用数形结合的思想解决问题.例题分析.反比例函数的概念()已知函数是反比例函数,①若它的图象在第二、四象限内,那么k②若随的增大而减小,那么kaby=—()已知一次函数a的图象经过第一、二、四象限,则函数x的图象位于第象限.k()若反比例函数经过点(T,),则一次函数$=-心+2的图象一定不经过第象限.ay=—()已知a・bVO,点(a,b)在反比例函数x的图象上,则直线y=不经过的象限是().•第一象限•第二象限•第三象限•第四象限k__()若(,)和(,-加是反比例函数疋图象上的两点,则一次函数k的图象经过()••第一、二、三象限•第一、二、四象限•第一、三、四象限•第二、三、四象限_k()已知函数"3D和八一匚(山0),它们在同一坐标系内的图象大致是(•)图象和性5()在反比例函数F的图象上有两点"(引曲,月(可,对,且兀>也>0,则儿_兀的值为().•正数•负数•非正数•非负数__]丄()在函数I疋(为常数)的图象上有三个点(7X),匕了血1,乃),则函数值”、此、乃的大小关系是()..兀V旳VX.兀V必VX•乃<旳<旳!_5__5()下列四个函数中:①y=^x:②尹=一乐;③,x;④,X.随的增大而减小的函数有().•个•个•个y=——函数的增减