初中数学教学中巧用面积法解题VIP免费

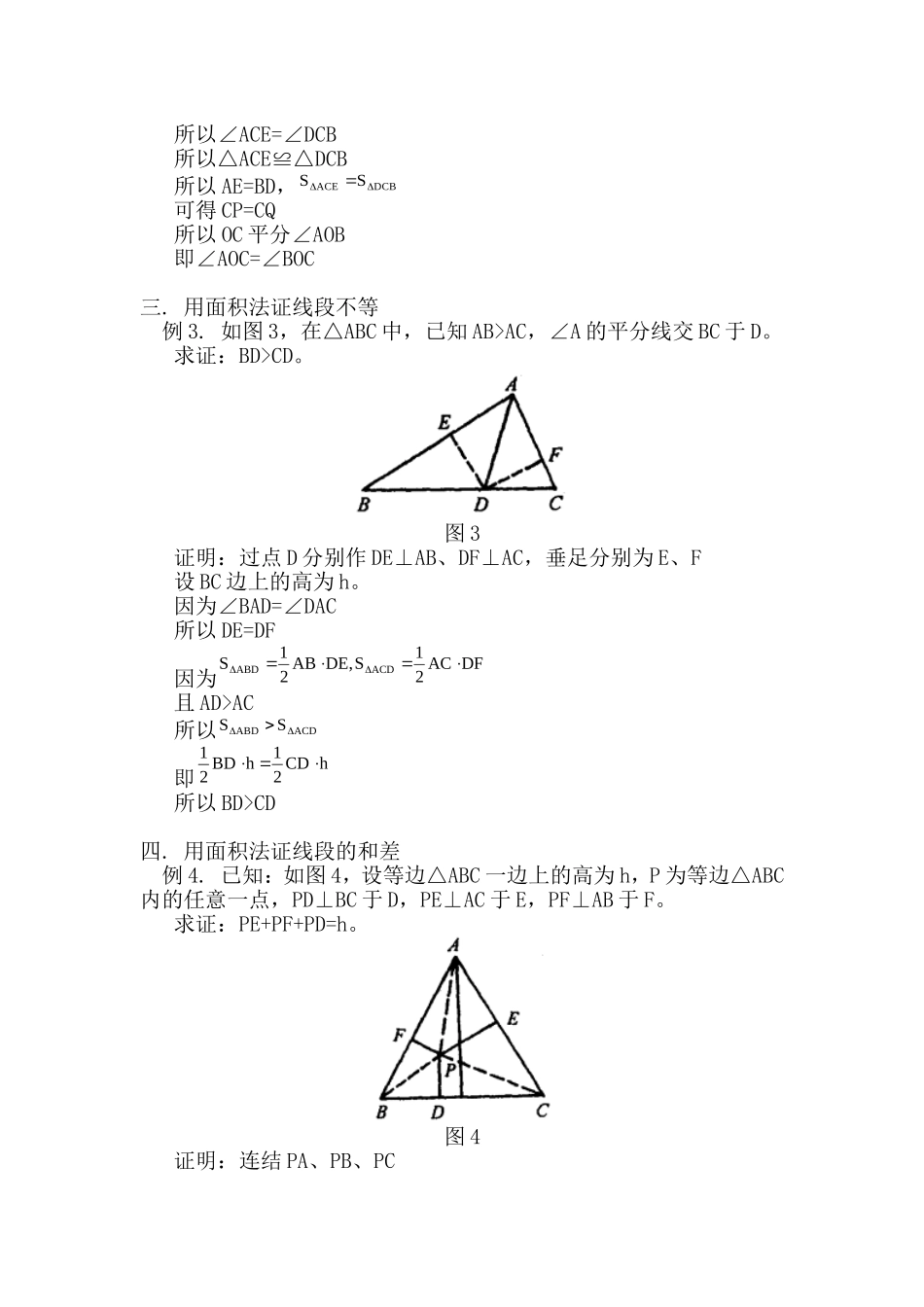
初中数学教学中巧用面积法解题许多数学问题，表面上看来似与面积无关，但灵活运用面积法，往往能使问题顺利获解，下面举例介绍面积法的运用。一.用面积法证线段相等例1.已知：如图1，AD是△ABC的中线，CF⊥AD于F，BE⊥AD交AD的延长线于E。求证：CF=BE。图1证明：连结EC，由BD=DC得，CDEBDEACDABDSS,SS，两式两边分别相加，得ACEABESS故CFAE21BEAE21所以BE=CF。注：直接由ACDABDSS得CFAD21BEAD21更简洁。二.用面积法证两角相等例2.如图2，C是线段AB上的一点，△ACD、△BCE都是等边三角形，AE、BD相交于O。求证：∠AOC=∠BOC。图2证明：过点C作CP⊥AE，CQ⊥BD，垂足分别为P、Q。因为△ACD、△BCE都是等边三角形，所以AC=CD，CE=CB，∠ACD=∠BCE，所以∠ACE=∠DCB所以△ACE≌△DCB所以AE=BD，DCBACESS可得CP=CQ所以OC平分∠AOB即∠AOC=∠BOC三.用面积法证线段不等例3.如图3，在△ABC中，已知AB>AC，∠A的平分线交BC于D。求证：BD>CD。图3证明：过点D分别作DE⊥AB、DF⊥AC，垂足分别为E、F设BC边上的高为h。因为∠BAD=∠DAC所以DE=DF因为DFAC21S,DEAB21SACDABD且AD>AC所以ACDABDSS即hCD21hBD21所以BD>CD四.用面积法证线段的和差例4.已知：如图4，设等边△ABC一边上的高为h，P为等边△ABC内的任意一点，PD⊥BC于D，PE⊥AC于E，PF⊥AB于F。求证：PE+PF+PD=h。图4证明：连结PA、PB、PC因为PEAC21S,PFAB21SAPCABP，PDBC21SBCP又BPCAPCABPABCSSSS所以PDBC21PEAC21PFAB21hBC21。因为△ABC是等边三角形所以PDPEPFh即PE+PF+PD=h五.用面积法证比例式或等积式例5.如图5，AD是△ABC的角的平分线。求证：DCBDACAB。图5证明：过D点作DE⊥AB，DF⊥AC，垂足分别为E、F。因为AD是△ABC的角的平分线，所以DE=DF，则有ACABSSACDABD。过A点作AH⊥BC，垂足为H，则有DCBDSSACDABD即DCBDACAB六.用面积比求线段的比例6.如图6，在△ABC中，已知BC、AC边上的中线AD、BF交于M。求证：AM21MD。图6证明：连结CM，过B作BG⊥AD交AD延长线于G，则MAFMCFBCFBAFSS,SS，所以MBCMABSS。又MBCMDCMBDS21SS，所以MABMBDS21S，AMBG21S,MDBG21SBAMMBD所以AM21MD。总结人：张廷伦2010年5月18日