相似三角形的性质VIP免费

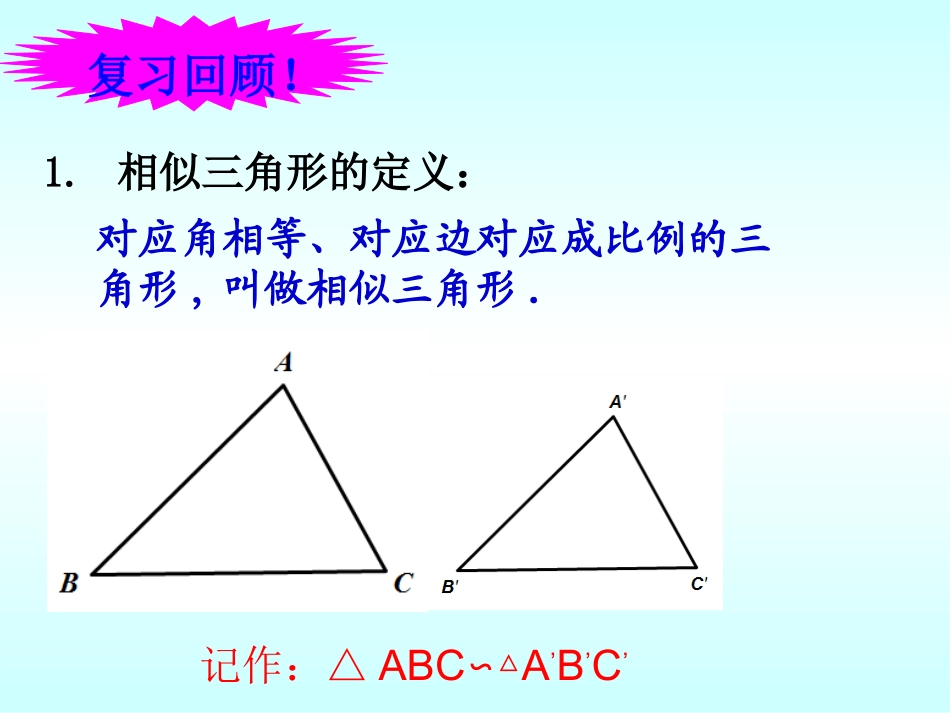
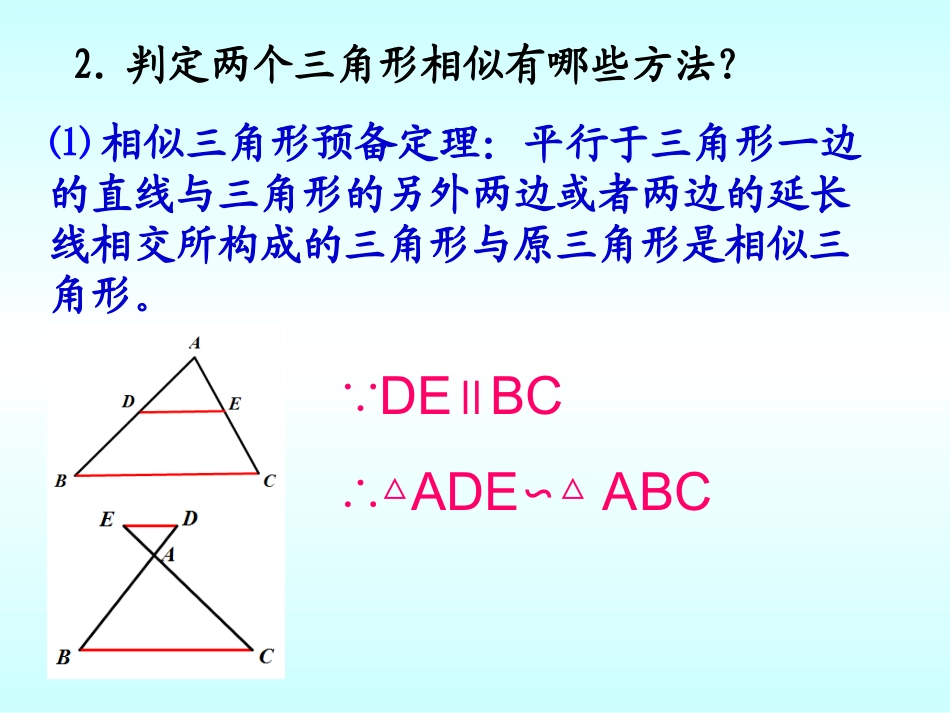
东坡二中校本教研执教老师：李红斌2015年11月4日复习回顾！1.相似三角形的定义：对应角相等、对应边对应成比例的三角形,叫做相似三角形.记作：△ABCA∽△,B,C,2.判定两个三角形相似有哪些方法？⑴相似三角形预备定理：平行于三角形一边的直线与三角形的另外两边或者两边的延长线相交所构成的三角形与原三角形是相似三角形。∵DEBC∥∴△ADEABC∽△⑵相似三角形判定定理1：两个角对应相等的两个三角形相似；∵∠A＝∠A’，∠B＝∠B’∴△ABCA’B’C’∽△⑶相似三角形判定定理2：两边对应成比例,且夹角相等的两个三角形相似；＇＇＇＇∽△△＝，＝∵＇＇＇＇CBAABCAAACCAABBA⑷相似三角形判定定理3：三边对应成比例的两个三角形相似.＇＇＇ACCAABBACB∽△A△ABC，∵＇＇＇＇BCCB＇＇3.相似三角形的性质：①相似三角形对应边成比例②相似三角形对应角相等＇＇＇，，，＇＇CCBBAABCCBACCAABBA＇＇＇＇＇＇＇，CB∽△A∵△ABC动动脑子相似三角形还有没有其它的性质呢？一个三角形除了三边和三角外，还有哪几条重要的线呢？这些线是不是也具有像边一样的性质呢？高、角平分线中线、新课探索？DBAABDCBBC、DAAD、kCBAABC相似吗与边上的高分别为其中相似比为∽如图问题,,,,:1CBAABC∽∵:解∴∠B=∠B′（）相似三角形的对应角相等.90BDAADB∵又.DBAΔΔABD∽（）两角对应相等,两三角形相似DAADBAAB∴(相似三角形的对应边成比例)k结论：相似三角形对应高的比等于相似比..____,,,,DAADCBBC、DAAD、kCBAABC则边上的中线分别为其中相似比为∽如图猜一猜，试一试，动动手问题2：结论：相似三角形对应中线的比等于相似比.∴＇BAAB＇CBBC＇＇＇＇＇＇的中线和是∵CBDBBCBD2121,，CB△A△ABCDAAD,＇＇＇CBAABC∽∵解：＇BBABABCBBCDBBD＇＇＇＇2121KBAABDAAD＇＇＇＇∽＇＇＇DB△A△ABD巩固知识，你会证明了吗？.____,,,,3DAADCABBAC、DAAD、kCBAABC则边上的角平分线分别为其中相似比为∽：如图问题角平分线和是∵＇＇＇＇＇CBA△ABCDAAD,＇＇＇＇＇＇，CABDABBACBAD2121＇＇＇CBA△ABC∽∵＇＇＇＇，BBCABBAC＇＇＇DABBADKBAABDAAD＇＇＇＇∽＇＇＇DBA△ABD解：结论：相似三角形对应角的角平分线的比等于相似比.CBAkACCACBBCBAAB证明：△ABC∽△问题4：已知△ABC∽△，且相似比为k。求证：△ABC、周长的比等于kCBACBAkACCBBACABCAB即△ABC、△的周长比等于相似比CBA∵∴∴结论：相似三角形对应角的周长的比等于相似比.看谁做的快问题5:两个相似三角形的面积与相似比之间有什么关系呢？延伸拓展，是否都一样？DABCD'C'A'B'如图已知△ABC∽△A´B´C´，且相似比为k，AD、A´D´分别是△ABC、△A´B´C´对应边BC、B´C´上的高，求证：2kSSCBAABC证明：∵△ABC∽△A´B´C´∴kCBBCkDAAD,∴22121kCBDABCADSSCBAABCDABCD'C'A'B'结论：相似三角形面积的比等于相似比的平方.小结一下，你学到了什么？1.相似三角形对应高的比等于相似比.2.相似三角形对应中线的比等于相似比.3.相似三角形对应角的角平分线的比等于相似比.4.相似三角形周长的比等于相似比.5.相似三角形面积的比等于相似比的平方.作业布置：课时优化：P61页随堂练习伟大的成绩和辛勤劳动是成正比例的，有伟大的成绩和辛勤劳动是成正比例的，有一分劳动就有一分收获，日积月累，从少到一分劳动就有一分收获，日积月累，从少到多，奇迹就可以创造出来。——鲁迅多，奇迹就可以创造出来。——鲁迅