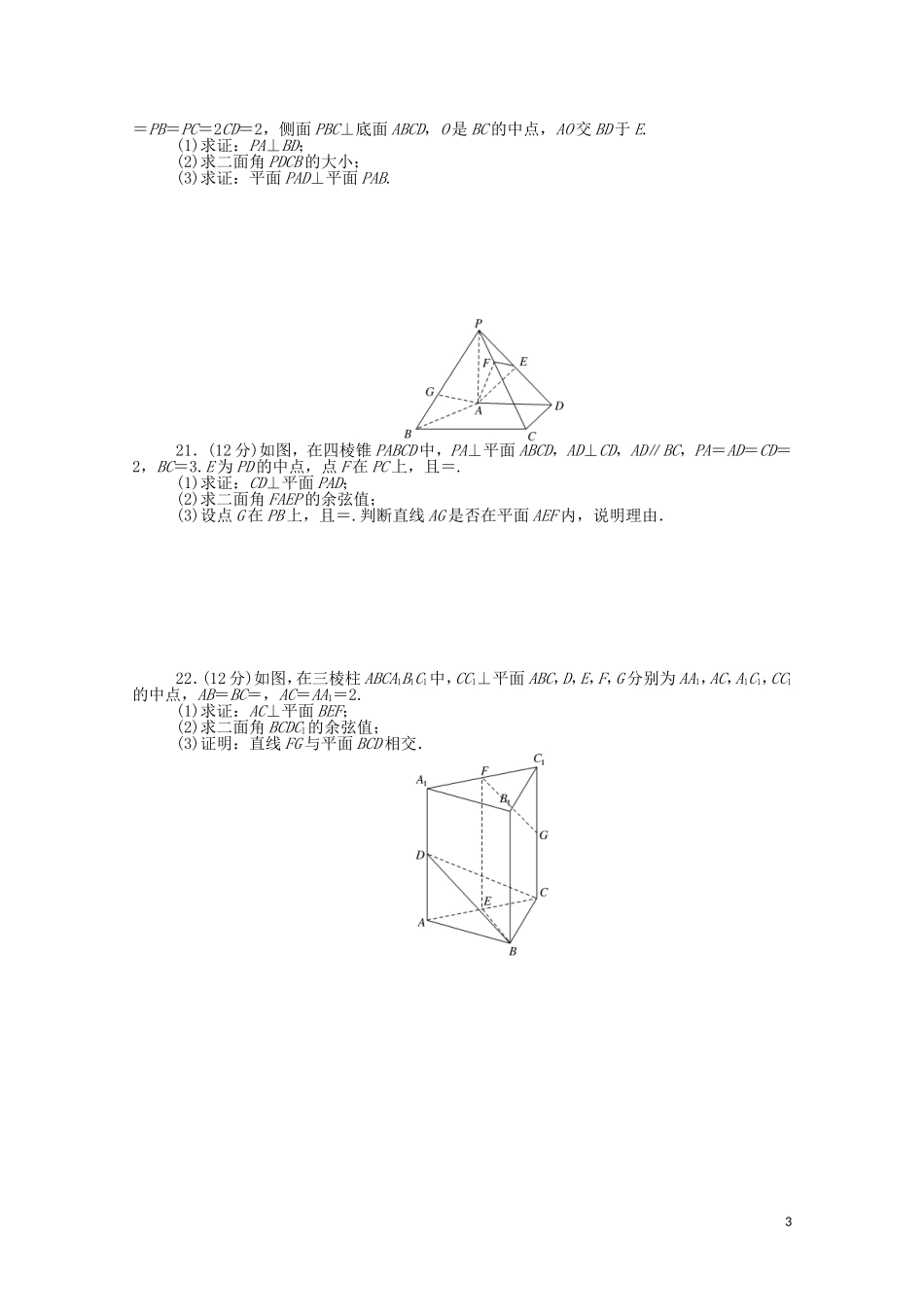
章末质量检测(一)空间向量与立体几何一、选择题(本大题共12个小题,每小题5分,共60分.在每小题给出的四个选项中,只有一项是符合题目要求的)1.以下四组向量:①a=(1,-2,1),b=(-1,2,-1);②a=(8,4,0),b=(2,1,0);③a=(1,0,-1),b=(-3,0,3);④a=,b=(4,-3,3).其中互相平行的是()A.②③B.①④C.①②④D.①②③④2.已知向量a=(2,-3,5)与b=(4,x,y)平行,则x,y的值为()A.6和-10B.-6和10C.-6和-10D.6和103.在四面体OABC中,点P为棱BC的中点.设OA=a,OB=b,OC=c,那么向量AP用基底{a,b,c}可表示为()A.-a+b+cB.-a+b+cC.a+b+cD.a+b+c4.正方体ABCDA1B1C1D1中,BB1与平面ACD1所成角的余弦值为()A.B.C.D.5.已知长方体ABCDA1B1C1D1,下列向量的数量积一定不为0的是()A.AD1·B1CB.BD1·ACC.AB·AD1D.BD1·BC6.已知A(-4,6,-1),B(4,3,2),则下列各向量中是平面AOB的一个法向量的是()A.(0,1,6)B.(-1,2,-1)C.(-15,4,36)D.(15,4,-36)7.四棱锥PABCD中,底面ABCD是平行四边形,AB=(2,-1,-4),AD=(4,2,0),AP=(-1,2,-1),则PA与底面ABCD的关系是()A.相交B.垂直C.不垂直D.成60°角8.已知正四棱锥SABCD的侧棱长与底面边长都相等,E是SB的中点,则AE与平面SBC所成的角的余弦值为()A.B.C.D.9.如图所示,在四面体PABC中,PC⊥平面ABC,AB=BC=CA=PC,那么二面角BAPC的余弦值为()A.B.C.D.10.已知四边形ABCD是边长为4的正方形,E,F分别是边AB,AD的中点,GC垂直于正方形ABCD所在平面,且GC=2,则点B到平面EFG的距离为()A.3B.C.D.11.已知四棱锥O-ABCD中,OA=a,OB=b,OC=c,点M在OA上,且OM=2MA,N为BC中点,则MN=()A.a-b+cB.a+b-cC.-a+b+cD.a+b-c12.将正方形ABCD沿对角线BD折成一个直二面角,点C到达点C1,则异面直线AB与C1D1所成角是()A.90°B.60°C.45°D.30°二、填空题(本大题共4个小题,每小题5分,共20分.把答案填在题中的横线上)13.若a=(2,-3,5),b=(-3,1,-4),则|a-2b|=__________.14.在空间直角坐标系中,已知a=(2,-1,3),b=(-4,2,x).若a⊥b,则x=________.15.如图,在空间四边形ABCD中,AC和BD为对角线,G为△ABC的重心,E是BD上一点,BE=3ED,以{AB,AC,AD}为基底,则GE=________.16.已知棱长为1的正方体ABCD-A1B1C1D1中,E是A1B1的中点,则直线AE与平面ABC1D1所成角的正弦值为________.三、解答题(本大题共6个小题,共70分.解答时应写出必要的文字说明、证明过程或演算步骤)17.(10分)在四棱锥PABCD中,底面ABCD是一直角梯形,∠BAD=90°,AD∥BC,AB=BC=a,AD=2a,且PA⊥底面ABCD,PD与底面成30°角.(1)若AE⊥PD,E为垂足,求证:BE⊥PD;(2)求异面直线AE与CD所成角的余弦值.18.(12分)如图,在四棱锥PABCD中,PA⊥底面ABCD,AD⊥AB,AB∥DC,AD=DC=AP=2,AB=1,点E为棱PC的中点.(1)证明:BE⊥DC;(2)求直线BE与平面PBD所成角的正弦值;(3)若F为棱PC上一点,满足BF⊥AC,求二面角FABP的余弦值.19.(12分)如图,在三棱锥PABC中,PA=PB=AB=2,BC=3,∠ABC=90°,平面PAB⊥平面ABC,D,E分别为AB,AC中点.(1)求证:DE∥平面PBC;(2)求证:AB⊥PE;(3)求二面角APBE的大小.20.(12分)如图,已知四棱锥PABCD的底面是直角梯形,∠ABC=∠BCD=90°,AB=BC2=PB=PC=2CD=2,侧面PBC⊥底面ABCD,O是BC的中点,AO交BD于E.(1)求证:PA⊥BD;(2)求二面角PDCB的大小;(3)求证:平面PAD⊥平面PAB.21.(12分)如图,在四棱锥PABCD中,PA⊥平面ABCD,AD⊥CD,AD∥BC,PA=AD=CD=2,BC=3.E为PD的中点,点F在PC上,且=.(1)求证:CD⊥平面PAD;(2)求二面角FAEP的余弦值;(3)设点G在PB上,且=.判断直线AG是否在平面AEF内,说明理由.22.(12分)如图,在三棱柱ABCA1B1C1中,CC1⊥平面ABC,D,E,F,G分别为AA1,AC,A1C1,CC1的中点,AB=BC=,AC=AA1=2.(1)求证:AC⊥平面BEF;(2)求二面角BCDC1的余弦值;(3)证明:直线FG与平面BCD相交.3章末质量检测(一)空间向量与立体几何1.解析:因为①a=(1,-2,1)=-b=-(-1,2...