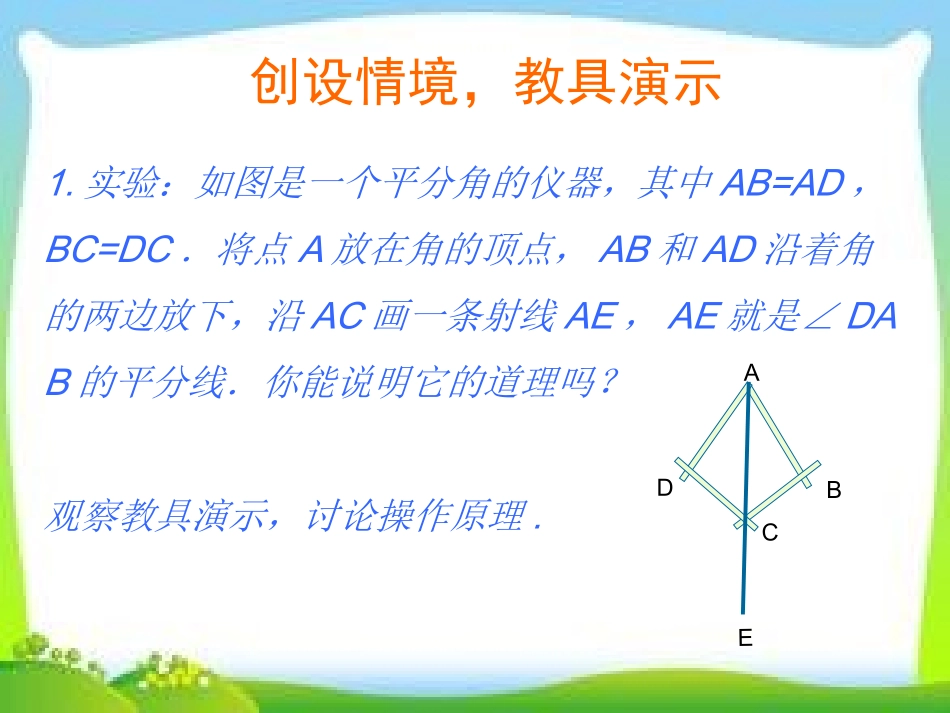
1.实验:如图是一个平分角的仪器,其中AB=AD,BC=DC.将点A放在角的顶点,AB和AD沿着角的两边放下,沿AC画一条射线AE,AE就是∠DAB的平分线.你能说明它的道理吗?观察教具演示,讨论操作原理.创设情境,教具演示DCBAE学习目标1.会用尺规作一个已知角的平分线.2.掌握角平分线的性质及应用.学习指导自学P48-49思考上面的内容,认真看书,独立自学,安静思考,把下面问题的答案记录下来,以备交流.1.思考:尺规作图作角平分线的理论依据:①作法第一步保证了.②作法第二步保证了.2.怎样证明OC平分∠AOB?3.P48下面思考栏中,通过几次测量,你发现了角平分线的什么性质?4.角平分线的性质的内容是,把这一命题改为“如果……那么……”的形式应为.5.结合图形,写出已知、求证,并证明角平分线的性质.自研共探1.自研下面请同学们围绕目标进行自学,挑战自己,通过自学达到目标.(时间:6分钟)2.共探(1)对子交流对子互说学习指导中1、2的内容.(2).小组交流组内成员互说角平分线的性质.对角平分线性质的证明过程.学情展示展示内容:1.思考:尺规作图作角平分线的理论依据:①作法第一步保证了.②作法第二步保证了.2.怎样证明OC平分∠AOB?3.P48下面思考栏中,通过几次测量,你发现了角平分线的什么性质?4.角平分线的性质的内容是,把这一命题改为“如果……那么……”的形式应为.5.结合图形,写出已知、求证,并证明角平分线的性质归纳总结1.本节课学习了什么?还有哪些疑问?2.角平分线性质是证明线段相等的一个重要方法,应用时要注意两点:一是不要漏掉垂直关系的书写;二是直接得到线段相等,不必再证明两个三角形全等而走弯路.3.对一个几何命题证明时,要按照以下步骤进行:①明确命题中的已知和求证.②根据题意,画出图形,并用数学符号表示已知和求证.③经过分析,找出由已知推出要证明的结论的途径,写出证明过程.巩固提升1.P51练习2.(必做)2.检测题(选做)检测题1.如图①,OP平分∠AOB,PCOA⊥于点C,PDOB⊥于D,则PC与PD的大小关系是().A、PC>PDB、PC=PDC、PC