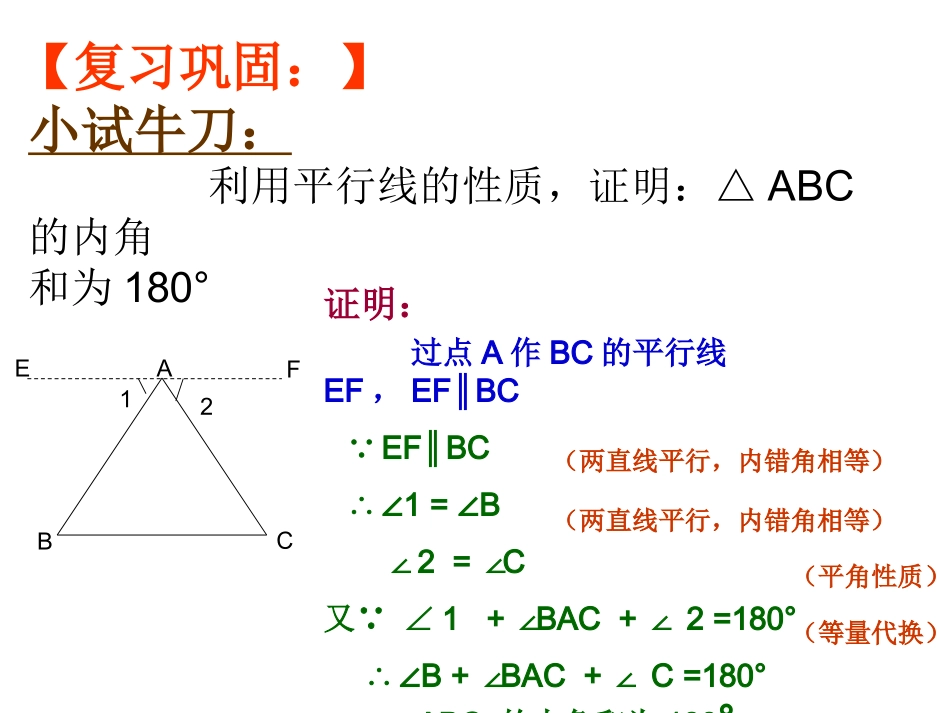
(1)平行线的性质:(1)、(2)、(3)【复习巩固:】小试牛刀:利用平行线的性质,证明:△ABC的内角和为180°ABC【提示:】过点A作BC的平行线EF,EF∥BC【复习巩固:】小试牛刀:利用平行线的性质,证明:△ABC的内角和为180°证明:过点A作BC的平行线EF,EF∥BC∵EF∥BC∴∠1=∠B∠2=∠C又∵∠1+∠BAC+2∠=180°∴∠B+∠BAC+C∠=180°∴△ABC的内角和为180°ABCEF12(两直线平行,内错角相等)(两直线平行,内错角相等)(平角性质)(等量代换)(2)平行线的判定:(1)、(2)、(3)【复习巩固:】小试牛刀:如图,已知ac⊥,bc⊥,试利用平行线的判定定理证明ab∥如图,已知ac⊥,bc⊥,试证明ab∥【新课导入:】abc12证明:∵ac⊥,bc⊥∴∠1=90°,∠2=90°∴∠1=2∠∴ab∥【推论:】在同一平面内,垂直于同一条直线的两条直线平行。【推论:】在同一平面内,垂直于同一条直线的两条直线平行。【即:】∵在同一平面内,ac⊥,b⊥c,∴ab∥【合作探究】探究一:如图所示,已知EFAB,CDAB,⊥⊥垂足分别为D,F,1=2,∠∠试判断DG与BC的位置关系,并说明理由。【合作探究:】探究一:如图所示,已知EFAB,CDAB,⊥⊥垂足分别为D,F,1=2,∠∠试判断DG与BC的位置关系,并说明理由。证明:∵在同一平面内,EFAB,CD⊥AB⊥∴EF∥CD∴∠1=3∠又∵∠1=2∠∴∠3=2∠∴DG∥BC【合作探究:】探究二:如图所示,CDFE⊥,BAFE⊥,垂足分别为点D、A,∠1=∠2。求证:CFEB∥CFDOEAB12【合作探究:】探究二:如图所示,CDFE⊥,BAFE⊥,垂足分别为点D、A,∠1=∠2。求证:CFEB∥证明:∵在同一平面内,CDFE⊥,BAFE⊥∴CD∥BA∴∠3=4∠又∵∠1=2∠∠3+1=FCB∠∠∠4+2=CBE∠∠∴∠FCB=CBE∠∴CF∥EB34【小结】