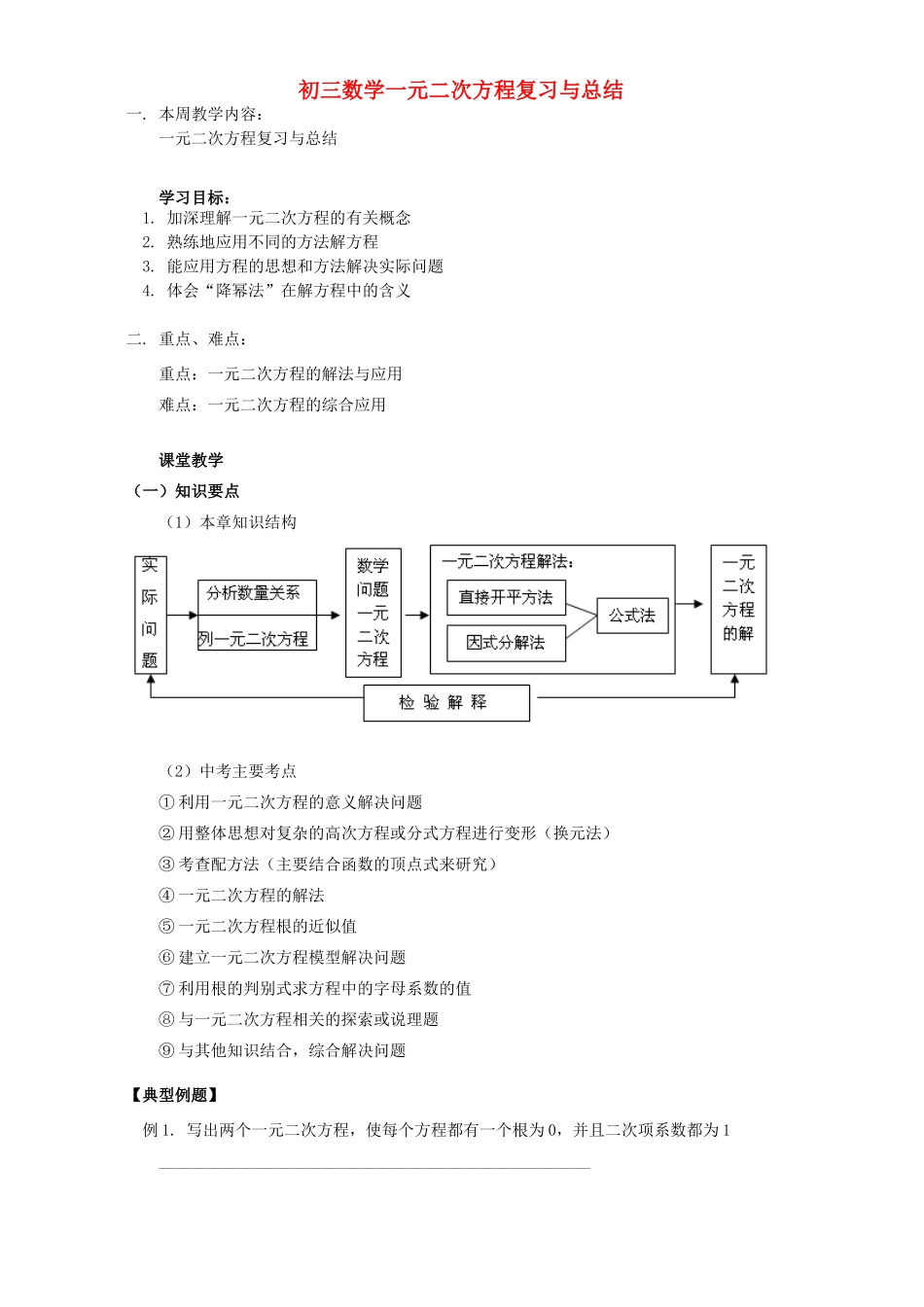
初三数学一元二次方程复习与总结一.本周教学内容:一元二次方程复习与总结学习目标:1.加深理解一元二次方程的有关概念2.熟练地应用不同的方法解方程3.能应用方程的思想和方法解决实际问题4.体会“降幂法”在解方程中的含义二.重点、难点:重点:一元二次方程的解法与应用难点:一元二次方程的综合应用课堂教学(一)知识要点(1)本章知识结构(2)中考主要考点①利用一元二次方程的意义解决问题②用整体思想对复杂的高次方程或分式方程进行变形(换元法)③考查配方法(主要结合函数的顶点式来研究)④一元二次方程的解法⑤一元二次方程根的近似值⑥建立一元二次方程模型解决问题⑦利用根的判别式求方程中的字母系数的值⑧与一元二次方程相关的探索或说理题⑨与其他知识结合,综合解决问题【典型例题】例1.写出两个一元二次方程,使每个方程都有一个根为0,并且二次项系数都为1_____________________________________________________解:答案不唯一,例如:x2=0x2-x=0例2.用换元法解方程x2-2x+=8,若设x2-2x=y,则原方程化为关于y的整数方程是()A.y2+8y-7=0B.y2-8y-7=0C.y2+8y+7=0D.y2-8y+7=0解:D。换元法的实质是整体思想的应用。例3.用配方法解方程:x2-4x-1=0解:利用配方法解一元二次方程的一般步骤是移项,二次项系数化为1,两边同时加上一次项系数一半的平方,左边化为完全平方式、利用平方的意义求解。例4.根据下表格的对应值判断方程ax2+bx+c=0(a≠0)一个解x的范围是()A.3<x<3.23B.3.23<x<3.24C.3.24<x<3.25D.3.25<x<3.26解:一元二次方程根近似值是深层次地理解方程的重要概念,在实际应用中,作用很大。例5.关于x的方程kx2+3x-1=0有实数根,则k的取值范围是()A.k≤B.k≥且k≠0C.k≥D.k>且k≠0解析:题目中仅仅说“有实数根”,没有说几个,可以是一个,也可以是两个,要讨论。例6.已知一元二次方程x2+2x-7=0的两个根为x1、x2,则x1+x2=()A.-2B.2C.-7D.7解:新课本中没有对两根和与积作深入的研究,但两根和与两根积很重要。例7.对于二次三项式x2-10x+36,小聪同学作出如下结论:无论x取什么实数它的值都不可能等于11,你是否同意他的说法?说说你的理由。解:不同意他的说法,应改为:无论x取什么实数,x2-10x+36的值都不可能小于11。例8.关于x的方程(m-1)x2-2(m-3)x+m+2=0有两个不相等的实数根,求m的取值范围。解:△=[-2(m-3)]2-4(m-1)(m+2)=-28m+44>0∴m<例9.如图,在宽为20m,长为32m的矩形试验田地中央,修筑同样宽的两条互相垂直的道路,把矩形田地分成四个相同的面积的小田块作良种试验田,要使每小块试验田的面积为135m2,道路的宽应为多少?错解:设道路的宽为xm(20-x)(32-x)=135×4∴x1=2,x2=50例10.如图①,一架长4m的梯子AB斜靠在与地面OM垂直的墙壁ON上,梯子与地面的倾斜角α为60°(1)求AO与BO的长(2)若梯子顶端A沿NO下滑,同时底端B沿OM向右滑行。①如图②设A点滑到C点,B点向右滑行到D点,并且AC:BD=2:3,试计算梯子顶端A沿NO下滑多少米?②如图③,当A点下滑到A′点,B点向右滑行到B′点时,梯子AB的中点P也随之运动到P′点,若∠POP′=15°求AA′的长度。解:(1)Rt△ABO中,∠O=90°,∠α=60°,∴∠OAB=30,又AB=4m,∴OB=2m,∴OA=m(2)①设AC=2x,BD=3x,在Rt△COD中OC=-2x,OD=2+3x,CD=4∴∴即A沿着NO下滑了m② P和P′分别是Rt△AOB和Rt△A′O′B′的斜边A′B′的中点。∴PA=PO,P′A′=P′O∴∠P′A′O-∠PAO=∠POP′=15° ∠PAO=30,∴∠P′A′O=45°∴A′O=A′B′×=∴AA′=OA-A′O=()m说明:本题综合考查直角三角形,一元二次方程与空间图形的相关知识,综合性很强。【模拟试题】(答题时间:30分钟)1.解一元二次方程x2-x-12=0,结果正确的是()A.x1=-4,x2=3B.x1=4,x2=-3C.x1=-4,x2=-3D.x1=4,x2=32.一元二次方程(1-k)x2-2x-1=0有两个不相等的实数根,则k的取值范围()A.k>2B.k<2且k≠1C.k<2D.k>2且k≠13.已知方程5y2+ky-6=0有一个根是2,则另一个根为,k...