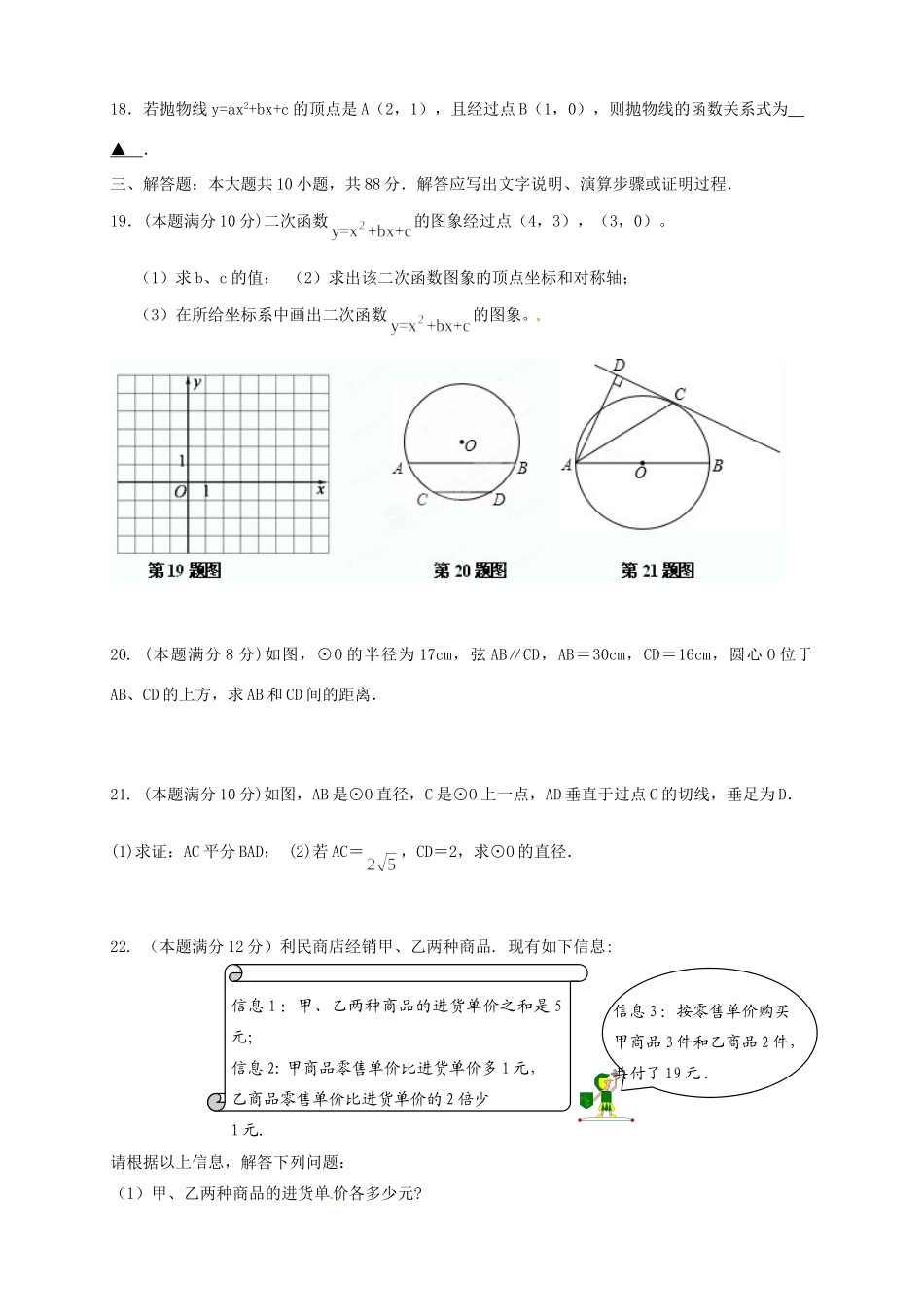
江苏省赣榆县汇文双语学校2013届九年级数学第二次质量检测试题(无答案)苏科版一、选择题(每小题3分,共30分)1.连云港市2010年平均房价为每平方米4000元.连续两年增长后,2012年平均房价达到每平方米5500元,设这两年平均房价年平均增长率为x,根据题意,下面所列方程正确的是(▲)A.5500(1+x)2=4000B.5500(1﹣x)2=4000C.4000(1﹣x)2=5500D.4000(1+x)2=55002.某学校准备修建一个面积为200平方米的矩形花圃,它的长比宽多10米,设花圃的宽为x米,则可列方程为(▲)A.x(x-10)=200B.2x+2(x-10)=200C.x(x+10)=200D.2x+2(x+10)=2003.将抛物线y=x2+1先向左平移2个单位,再向下平移3个单位,那么所得抛物线的函数关系式是(▲)A.y=(x+2)2+2B.y=(x+2)2-2C.y=(x-2)2+2D.y=(x-2)2-24.如图,已知抛物线的对称轴为,点A,B均在抛物线上,且AB与轴平行,其中点A的坐标为(0,3),则点B的坐标为(▲)A.(2,3)B.(3,2)C.(3,3)D.(4,3)5.如图,△ABC内接于⊙O,OD⊥BC于D,∠A=50°,则∠OCD的度数是(▲)A.40°B.45°C.50°D.60°6.如图,⊙O的半径为5,弦AB的长为8,M是弦AB上的动点,则线段OM长的最小值为.A.5B.4C..3D.2(▲)7.如果⊙A的半径是4cm,⊙B的半径是10cm,圆心距AB=8cm,那么这两个圆的位置关系是A.外离B.外切C.相交D.内切(▲)8.如图,已知:Rt△ABC的斜边AB=13cm,一条直角边AC=5cm,以直线BC为轴旋转一周得一个圆锥,则这个圆锥的表面积为(▲)A.65∏cm2B.90∏cm2C.156∏cm2D.300∏cm29.如图,AB是⊙O的直径,C.D是⊙O上一点,∠CDB=20°,过点C作⊙O的切线交AB的延长线于点E,则∠E等于(▲)10.二次函数的图象如图所示,则一次函数与反比例函数在同一坐标系内的图象大致为(▲)二、填空题(每题4分,共32分)11.如图,圆周角∠BAC=65°,分别过B,C两点作⊙O的切线,两切线相交与点P,则∠BPC=▲°.12.如图,AD,AC分别是⊙O的直径和弦.且∠CAD=30°.OB⊥AD,交AC于点B.若OB=5,则BC的长等于▲。13.抛物线的对称轴是直线,则b的值为▲.14.已知⊙O1与⊙O2的半径分别是方程的两根,且,若这两个圆相切,则t=▲.15.已知二次函数y=2(x﹣3)2+1.下列说法:①其图象的开口向下;②其图象的对称轴为直线x=﹣3;③其图象顶点坐标为(3,﹣1);④当x<3时,y随x的增大而减小.则其中说法正确的有▲16.已知扇形的面积为12,半径是6,则它的圆心角是▲.17.设A,B,C是抛物线上的三点,则,,的大小关系为▲18.若抛物线y=ax2+bx+c的顶点是A(2,1),且经过点B(1,0),则抛物线的函数关系式为▲.三、解答题:本大题共10小题,共88分.解答应写出文字说明、演算步骤或证明过程.19.(本题满分10分)二次函数的图象经过点(4,3),(3,0)。(1)求b、c的值;(2)求出该二次函数图象的顶点坐标和对称轴;(3)在所给坐标系中画出二次函数的图象。20.(本题满分8分)如图,⊙O的半径为17cm,弦AB∥CD,AB=30cm,CD=16cm,圆心O位于AB、CD的上方,求AB和CD间的距离.21.(本题满分10分)如图,AB是⊙O直径,C是⊙O上一点,AD垂直于过点C的切线,垂足为D.(1)求证:AC平分BAD;(2)若AC=,CD=2,求⊙O的直径.22.(本题满分12分)利民商店经销甲、乙两种商品.现有如下信息:请根据以上信息,解答下列问题:(1)甲、乙两种商品的进货单价各多少元?信息1:甲、乙两种商品的进货单价之和是5元;信息2:甲商品零售单价比进货单价多1元,乙商品零售单价比进货单价的2倍少1元.信息3:按零售单价购买甲商品3件和乙商品2件,共付了19元.(2)该商店平均每天卖出甲商品500件和乙商品300件.经调查发现,甲、乙两种商品零售单价分别每降0.1元,这两种商品每天可各多销售100件.为了使每天获取更大的利润,商店决定把甲、乙两种商品的零售单价都下降m元.在不考虑其他因素的条件下,当m定为多少时,才能使商店每天销售甲、乙两种商品获取的利润最大?每天的最大利润是多少?23.(本题满分12分)国家和地方政府为了提高农民种粮的积极性,每亩地每年发放种粮补贴120元,种粮大户老王今年种了150亩地,计划...