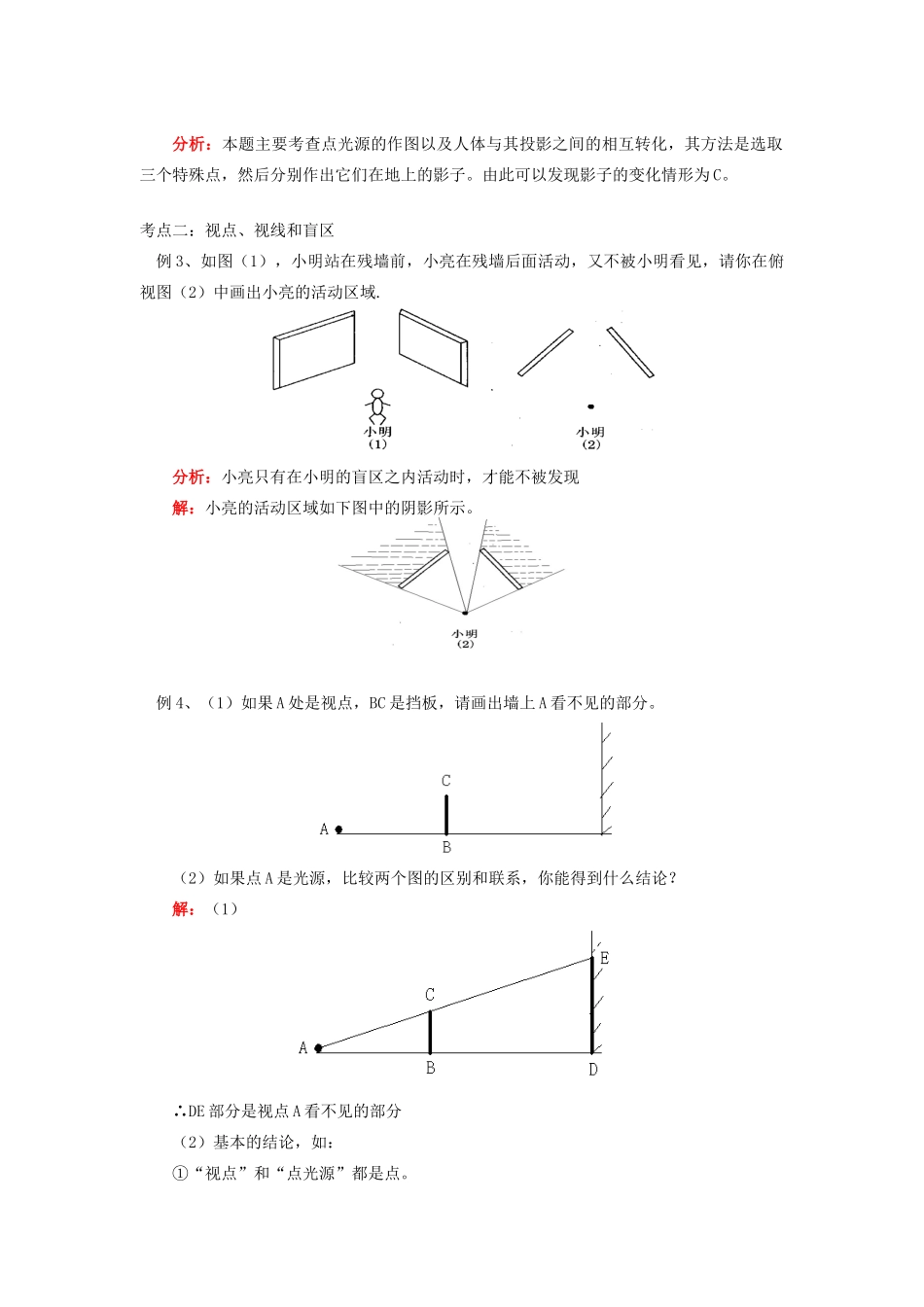
九年级数学第四章光与影子;本章回顾与思考北师大版【本讲教育信息】一、教学内容灯光与影子,本章的知识回顾二、教学目标1、经历实践、探索的过程,了解中心投影的含义,体会灯光下物体的影子在生活中的运用,体会灯光投影在生活中的实际价值。2、通过观察、想象,能根据灯光来辨别物体的影子,初步进行中心投影条件下物体与其投影之间的相互转化;3、能区别平行投影与中心投影条件下物体的投影;4、通过相互间的合作与交流,进一步发展学生合作交流的能力和数学表达能力;三、知识要点1、中心投影:探照灯、手电筒、路灯和台灯的光线可以看成是从一点发出的,像这样的光线所形成的投影称为中心投影2、视点:眼睛的位置称为视点。3、视线:由视点发出的线称为视线。4、盲区:看不到的地方称为盲区。5、单元知识结构四、重点难点1、了解中心投影,利用中心投影的概念,根据物体的影子画出光源所在的位置。2、中心投影和平行投影的区别和联系。3、了解视点、视线和盲区的含义,会根据此含义解释日常生活中的现象。【典型例题】考点一:中心投影例1、请你确定下图中路灯灯泡的位置,并用线段表示小明在该路灯下的影长。分析:过左边树的顶端及其影子的顶端作一条直线,再过另一棵树的顶端及影子的顶端作一条直线,两线相交于点O。则点O即为路灯灯泡所在的位置。过点O及小明的头顶作出直线,则线段AB即为小明的影长。解:如图所示,点O为路灯灯泡的位置,线段AB即为小明的影长。例2、如图,晚上在路灯下散步,在小亮由A处走到B处这一过程中,他在地上的影子()A.逐渐变短B.逐渐变长C.先变短后变长D.先变长后变短分析:本题主要考查点光源的作图以及人体与其投影之间的相互转化,其方法是选取三个特殊点,然后分别作出它们在地上的影子。由此可以发现影子的变化情形为C。考点二:视点、视线和盲区例3、如图(1),小明站在残墙前,小亮在残墙后面活动,又不被小明看见,请你在俯视图(2)中画出小亮的活动区域.分析:小亮只有在小明的盲区之内活动时,才能不被发现解:小亮的活动区域如下图中的阴影所示。例4、(1)如果A处是视点,BC是挡板,请画出墙上A看不见的部分。(2)如果点A是光源,比较两个图的区别和联系,你能得到什么结论?解:(1)∴DE部分是视点A看不见的部分(2)基本的结论,如:①“视点”和“点光源”都是点。②“视线”和“光线”都是光线。③“盲区”实际上就是把“视点”看成“点光源”,“光线”照不到的地方。“盲区”和“影子”本质上是一样的。考点三:太阳光与影子的应用例5、如图,AB和DE是直立在地面上的两根立柱,AB=5米,某一时刻AB在太阳光下的投影BC=3米。(1)请在图中画出此时DE在太阳光下的投影。(2)在测量AB的投影时,同时测出DE在阳光下的投影长为6米,请计算出DE的长。分析:(1)连接AC,则AC就是太阳光的光线,因为太阳光是平行光线,作DF∥AC,则EF就是DE在太阳光下的投影。(2)根据相似三角形,对应边成比例,可求得DE的长解:(1)如下图所示(2)由题可知△ABC∽△DEF∴(米)答:DE的长是10米。考点四:灯光与影子的应用例6、如图,路灯的灯光距离灯杆50cm,竖直的木棒长为100cm,且在灯光下的影长为150cm,已知木棒距离灯杆为800cm,求灯泡距离地面有多高?分析:如图所示,可以抽象地看成两个三角形,并且,这两个三角形相似。再由相似三角形对应边成比例可以求出灯泡距离地面的高度解:设灯泡距离地面的高度为xcm根据题意可得:解得x=600答:灯泡距离地面600cm高。【方法总结】通过生活中的实例,让学生体会到生活中的灯光与影子的规律性,将抽象的实物图转化到数学的图形上来,利用数形结合来解题。【预习导学方案】第五章第1~2节反比例函数及其图像、性质(一)预习前知1、反比例函数的概念2、反比例函数的图象3、反比例函数的性质(二)预习导学探索任务1:反比例函数的概念(一般地,如果两个变量x、y之间的关系可以表示成y=(k为常数,k≠0)的形式,那么称y是x的反比例函数.从y=中可知x作为分母,所以x不能为零.)反思:反比例函数的含义,能否根据已知条件列出反比例函数的表达式探索任务2:反比例函数的图象下图画出了...