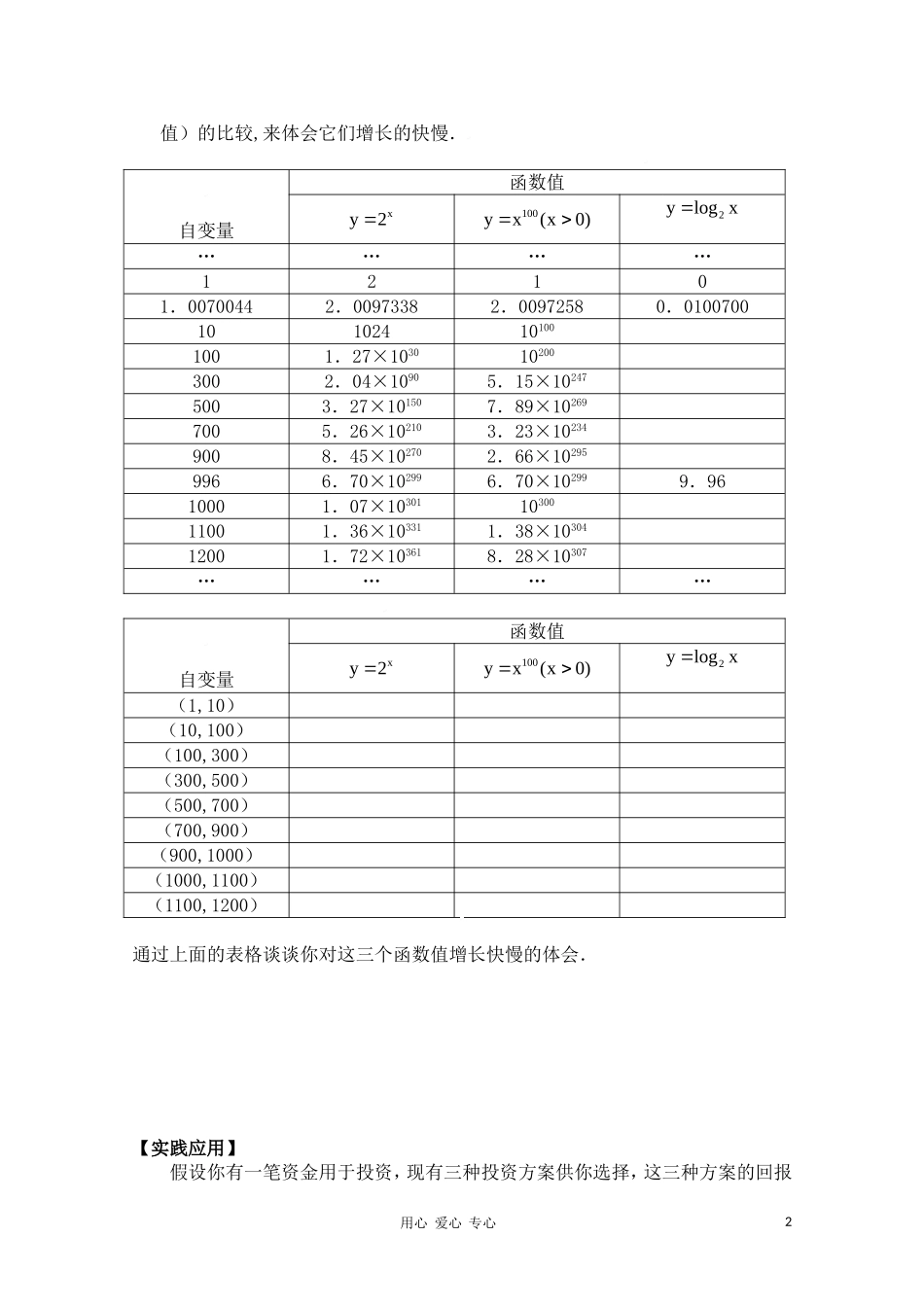
普通高中课程标准实验教科书[北师版]–必修1第三章指数函数与对数函数§3.6指数函数、幂函数、对数函数增长的比较(导学案)[学习目标]1、知识与技能会利用计算工具,比较指数函数、幂函数和对数函数的增长快慢.2、过程与方法(1)借助表格和图形了解指数函数的图像、幂函数的图像和对数函数的图像之间的关系以及变化.(2)学会类比研究问题,利用数性结合的思想研究函数的性质.3、情感.态度与价值观通过学习指数函数、幂函数的图像和对数函数的图像对比研究函数的增长快慢,在学习的过程中体会“指数爆炸”的含义,增强学习函数的积极性和自信心.[学习重点]:列表观察指数函数的图像、幂函数的图像和对数函数的图像的增长快慢[学习难点]:指数函数的图像、幂函数的图像和对数函数的图像的增长差异.[学习过程]:【自主学习】请同学们在同一坐标系中画出函数x22y2,yx,ylogx的图像,并观察比较函数图像的变化.你能判断出哪个函数的函数值随x的增长速度增长的比较快吗?谈谈你的体会。【互动探究】提出问题:当a1时,指数函数xya是增函数,并且当a越大时,其函数值的增长就越快.当a1时,指数函数aylogx是增函数,并且当a越大时,其函数值的增长就越快.当x0,n1时,幂函数nyx显然也是增函数,并且当n越大时,其函数值的增长就越快.那么对于这三种增加的函数,它们的函数值的增长快慢有何差别呢?我们通过对三个具体函数xy2,100yx(x0),2ylogx的函数值(取近似用心爱心专心1值)的比较,来体会它们增长的快慢.1.完成下表(借助科学计算器或设计程序通过计算机完成).自变量函数值xy2100yx(x0)2ylogx…………12101.00700442.00973382.00972580.0100700101024101001001.27×1030102003002.04×10905.15×102475003.27×101507.89×102697005.26×102103.23×102349008.45×102702.66×102959966.70×102996.70×102999.9610001.07×103011030011001.36×103311.38×1030412001.72×103618.28×10307…………2.利用上表中的数据完成下表自变量函数值xy2100yx(x0)2ylogx(1,10)(10,100)(100,300)(300,500)(500,700)(700,900)(900,1000)(1000,1100)(1100,1200)通过上面的表格谈谈你对这三个函数值增长快慢的体会.【实践应用】假设你有一笔资金用于投资,现有三种投资方案供你选择,这三种方案的回报用心爱心专心2如下:方案一:每天回报40元;方案二:第一天回报10元,以后每天比前一天多回报10元;方案三:第一天回报0.4元,以后每天的回报比前一天翻一番.请问,你会选择哪种投资方案?【巩固练习】1、0.32,log20.3,20.3这三个数之间大小关系是()A.0.32<20.3<log20.3;B.0.32<log20.3<20.3;C.log20.3<20.3<0.32;D.log20.3<0.32<20.3;2、作图像,试比较函数y=4x,y=x4,y=log4x的增长情况.【课堂小结】请同学们谈谈本节课有什么收获?用心爱心专心3