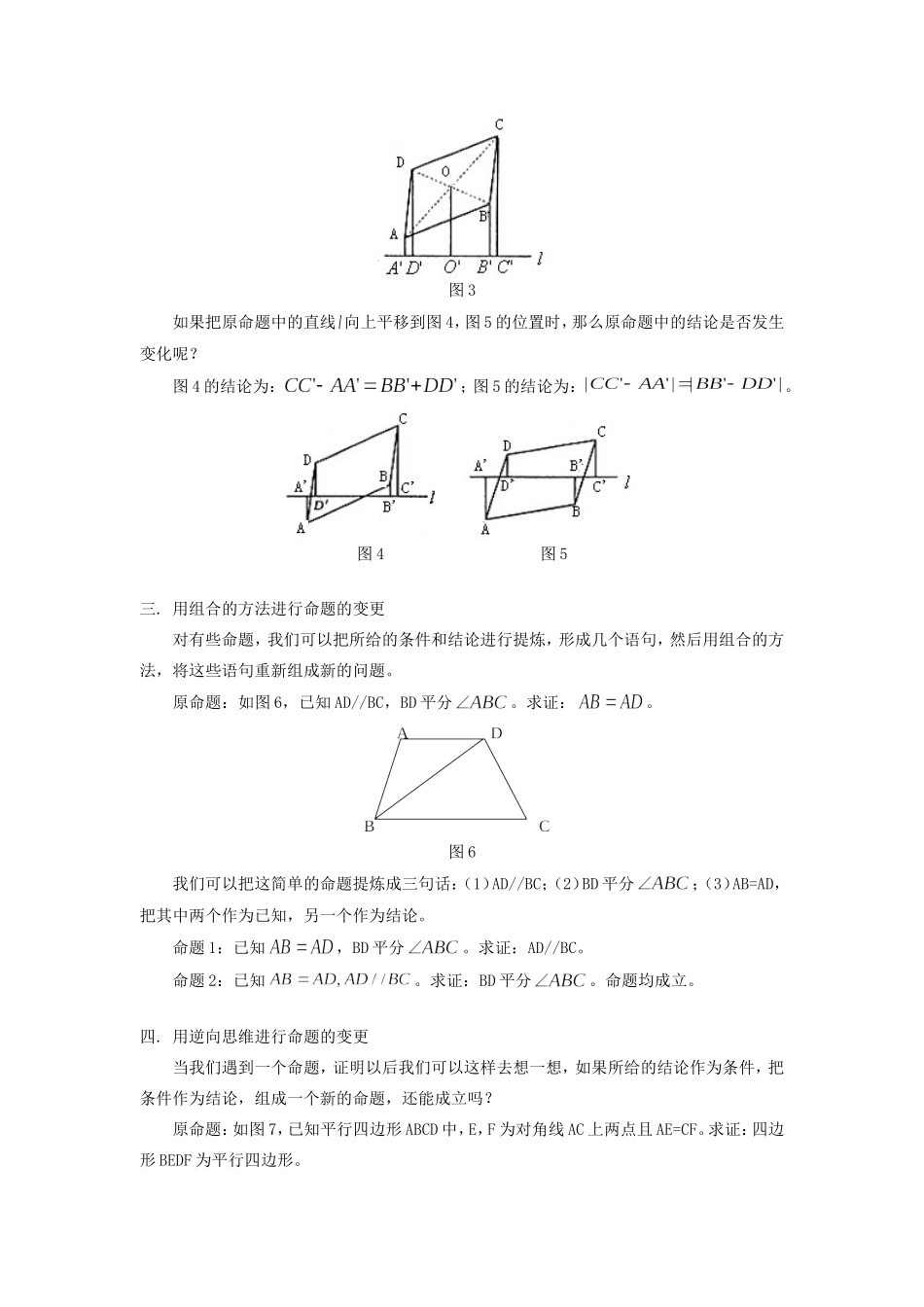
初中数学平面几何中的命题变更新课程标准的的实施,给我们的课堂学习的模式带来变革,对我们的课堂学习提出了新的要求。在学习平面几何的过程中,我们应在老师的指导下,自己去尝试设计问题、解决问题。在课本知识的基础之上通过一系列的变换进行命题的变更。一.用类比的方法进行命题的变更一个命题在某种情境中成立,我们可以通过类比的办法去想一想在另一个类似的情境中是否成立,从而完成了命题的变更。原命题:如图1,已知点M为正方形ABCD的边AB所在直线上任意一点(点A、B除外),,且与的邻补角的平分线交于N。求证:DM=MN。对于命题“M为正方形ABCD的边AB所在直线上任意一点”,我们可以通过类比,想象如果把“正方形ABCD”换成“正三角形ABC”,结论成立不成立呢?当然其他条件也要作适当的调整。图1命题:如图2,已知点M为正三角形ABC的边BC所在直线上任意一点(点B、C除外),MN与AM所成的角为,且与的邻补角的平分线交于N。求证:AM=MN。这个命题成立。图2二.用运动的观点进行命题的变更有些命题,它的图形是由一些图形组合起来的或是一个比较特殊的图形,我们可以抓住某一点或几个部分之间,通过运动的观点变化为一个新的图形,从而探索命题在新的图形中可以得到什么新的命题,达到命题变更的目的。原命题:已知:如图3,从平行四边形ABCD的顶点A,B,C,D向形外的任意直线作垂线垂足分别为,,探讨:有何数量关系?结论:。图3如果把原命题中的直线向上平移到图4,图5的位置时,那么原命题中的结论是否发生变化呢?图4的结论为:;图5的结论为:。图4图5三.用组合的方法进行命题的变更对有些命题,我们可以把所给的条件和结论进行提炼,形成几个语句,然后用组合的方法,将这些语句重新组成新的问题。原命题:如图6,已知AD//BC,BD平分。求证:。图6我们可以把这简单的命题提炼成三句话:(1)AD//BC;(2)BD平分;(3)AB=AD,把其中两个作为已知,另一个作为结论。命题1:已知,BD平分。求证:AD//BC。命题2:已知。求证:BD平分。命题均成立。四.用逆向思维进行命题的变更当我们遇到一个命题,证明以后我们可以这样去想一想,如果所给的结论作为条件,把条件作为结论,组成一个新的命题,还能成立吗?原命题:如图7,已知平行四边形ABCD中,E,F为对角线AC上两点且AE=CF。求证:四边形BEDF为平行四边形。图7结合图形,我们可以这样来想,如果告诉你的是内部的四边形BEDF为平行四边形的话,那外边的四边形ABCD是否一定是平行四边形?命题:已知平行四边形BEDF,E,F为四边形ABCD对角线AC所在直线上两点且AE=CF。求证:四边形ABCD为平行四边形。命题成立。