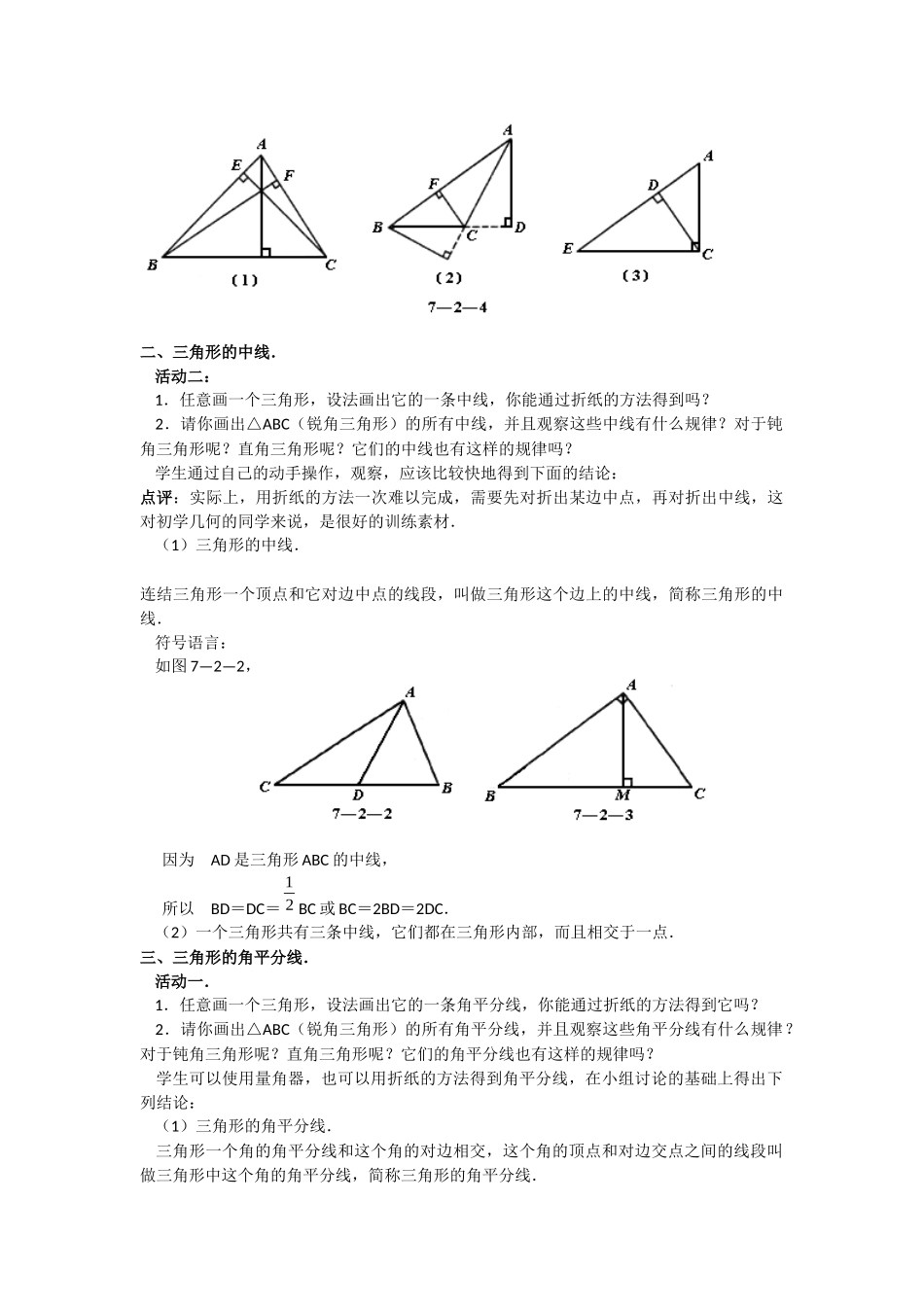
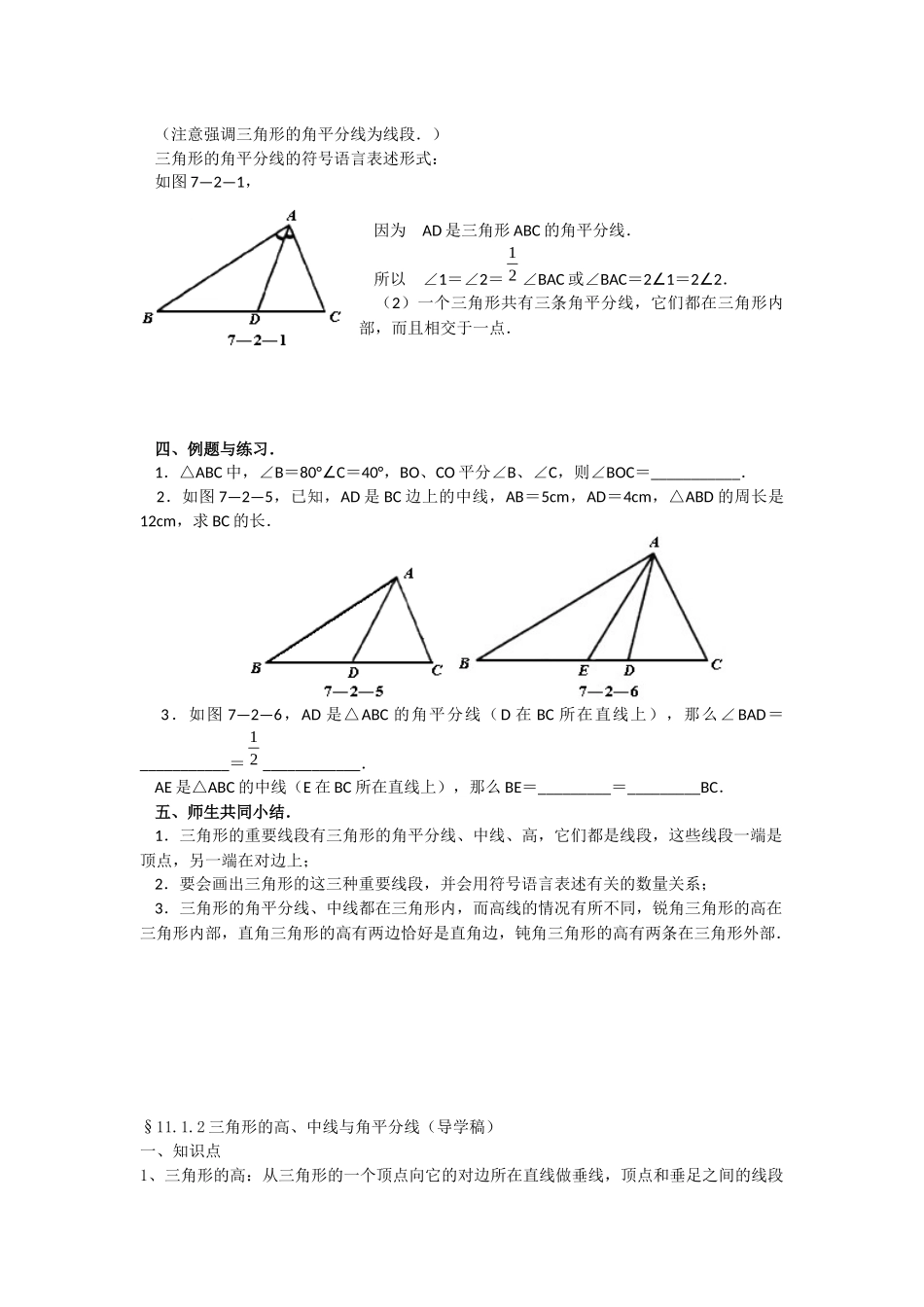
§11.1.2三角形的高、中线和角平分线·教学设计教学目标1.理解三角形的高、角平分线、中线的概念;2.能正确地画出一个三角形的高、角平分线和中线,并会用符号语言表述三角形的高、角平分线和中线的有关数量关系;3.逐步提高观察能力、语言表达能力以及基本作图能力.教学重点难点1.三角形的高、角平分线和中线的理解和应用;2.三角形高的画法及三角形中三条重要线段的符号语言表述方法.教学过程一、三角形的高.师:过三角形的一个顶点A,你能画出它的对边BC的垂线吗?试试看,你准行!1.三角形的高.从三角形的一个顶点向它的对边所在直线做垂线,顶点和垂足之间的线段叫做三角形的高线,简称三角形的高.如图7—2—3,因为AM是BC边上的高,所以∠AMB=∠AMC=90°.2.做一做:每人准备一个锐角三角形纸片:(1)你能画出这个三角形的高吗?你能用折纸的方法得到它吗?(2)这三条高之间有怎样的位置关系呢?(小组讨论交流.)结论:锐角三角形的三条高在三角形的内部且交于一点.3.议一议:每人画出一个直角三角形和一个钝角三角形.(1)画出直角三角形的三条高,并观察它们有怎样的位置关系?(2)你能折出钝角三角形的三条高吗?你能画出它们吗?(3)钝角三角形的三条高交于一点吗?它们所在的直线交于一点吗?[(如图7—2—4(1)(2)(3).]小组讨论交流.结论:(1)直角三角形的三条高交于直角顶点处.(2)钝角三角形的三条高所在直线交于一点,此点在三角形的外部.二、三角形的中线.活动二:1.任意画一个三角形,设法画出它的一条中线,你能通过折纸的方法得到吗?2.请你画出△ABC(锐角三角形)的所有中线,并且观察这些中线有什么规律?对于钝角三角形呢?直角三角形呢?它们的中线也有这样的规律吗?学生通过自己的动手操作,观察,应该比较快地得到下面的结论:点评:实际上,用折纸的方法一次难以完成,需要先对折出某边中点,再对折出中线,这对初学几何的同学来说,是很好的训练素材.(1)三角形的中线.连结三角形一个顶点和它对边中点的线段,叫做三角形这个边上的中线,简称三角形的中线.符号语言:如图7—2—2,因为AD是三角形ABC的中线,所以BD=DC=21BC或BC=2BD=2DC.(2)一个三角形共有三条中线,它们都在三角形内部,而且相交于一点.三、三角形的角平分线.活动一.1.任意画一个三角形,设法画出它的一条角平分线,你能通过折纸的方法得到它吗?2.请你画出△ABC(锐角三角形)的所有角平分线,并且观察这些角平分线有什么规律?对于钝角三角形呢?直角三角形呢?它们的角平分线也有这样的规律吗?学生可以使用量角器,也可以用折纸的方法得到角平分线,在小组讨论的基础上得出下列结论:(1)三角形的角平分线.三角形一个角的角平分线和这个角的对边相交,这个角的顶点和对边交点之间的线段叫做三角形中这个角的角平分线,简称三角形的角平分线.(注意强调三角形的角平分线为线段.)三角形的角平分线的符号语言表述形式:如图7—2—1,因为AD是三角形ABC的角平分线.所以∠1=∠2=21∠BAC或∠BAC=21∠=22∠.(2)一个三角形共有三条角平分线,它们都在三角形内部,而且相交于一点.四、例题与练习.1.△ABC中,∠B=80°∠C=40°,BO、CO平分∠B、∠C,则∠BOC=___________.2.如图7—2—5,已知,AD是BC边上的中线,AB=5cm,AD=4cm,△ABD的周长是12cm,求BC的长.3.如图7—2—6,AD是△ABC的角平分线(D在BC所在直线上),那么∠BAD=___________=21____________.AE是△ABC的中线(E在BC所在直线上),那么BE=_________=_________BC.五、师生共同小结.1.三角形的重要线段有三角形的角平分线、中线、高,它们都是线段,这些线段一端是顶点,另一端在对边上;2.要会画出三角形的这三种重要线段,并会用符号语言表述有关的数量关系;3.三角形的角平分线、中线都在三角形内,而高线的情况有所不同,锐角三角形的高在三角形内部,直角三角形的高有两边恰好是直角边,钝角三角形的高有两条在三角形外部.§11.1.2三角形的高、中线与角平分线(导学稿)一、知识点1、三角形的高:从三角形的一个顶点向它...