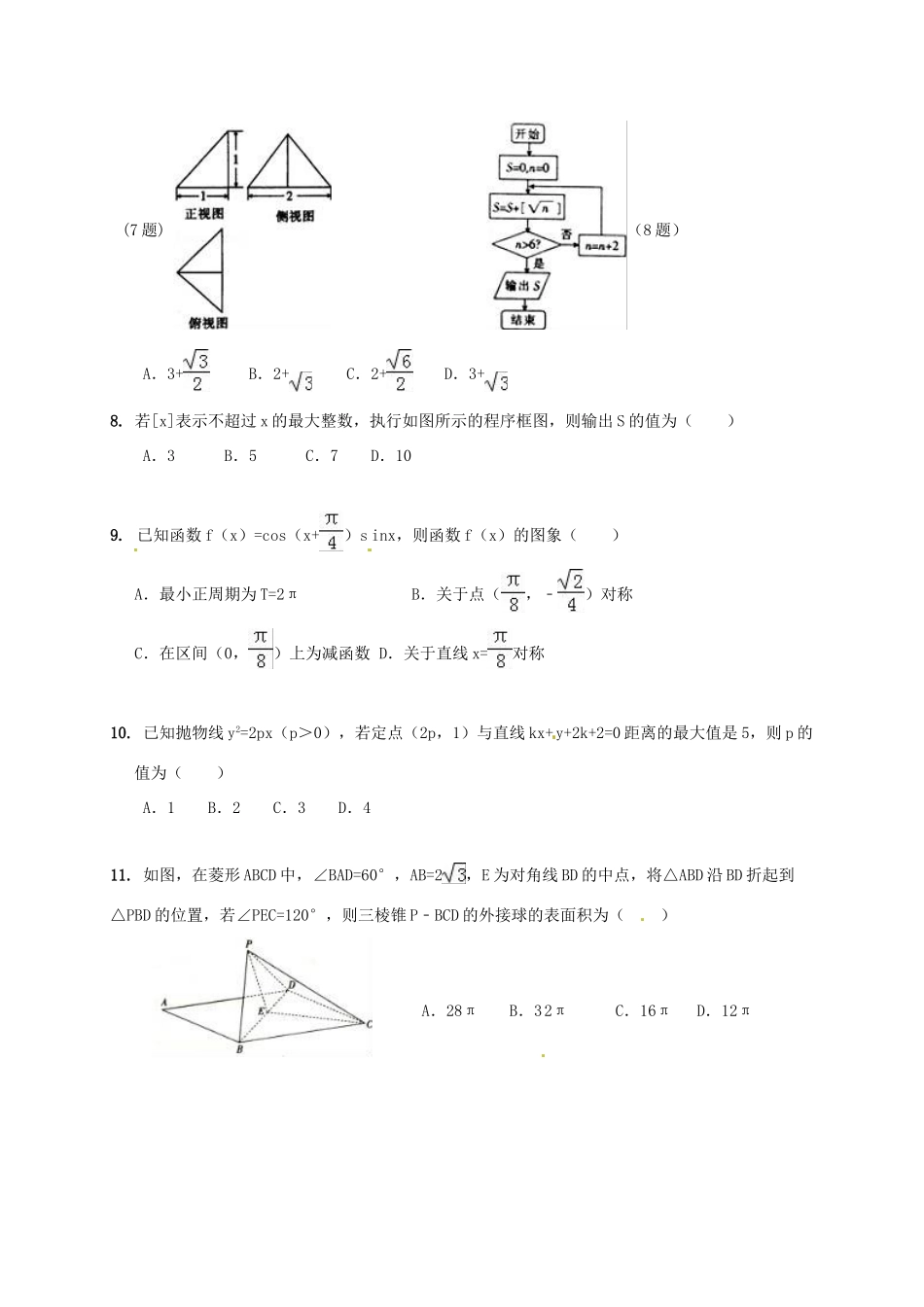
山西省临汾市2017届高三数学4月月考试题文一、选择题(本大题共12小题,每小题5分,共60分。在每小题给出的四个选项中,只有一项是符合题目要求的)1.集合A={x|0<x≤3},B={x|x2<4},则集合A∪B等于()A.(﹣∞,﹣2)B.(﹣2,3]C.(0,+∞)D.(﹣∞,3)2.设i是虚数单位,若复数是纯虚数,则a的值为()A.﹣B.﹣C.D.3.下列函数为奇函数的是()A.2x﹣B.x3sinxC.2cosx+1D.x2+2x4.已知变量x,y满足,则z=2x+2y的最小值为()A.﹣1B.0C.1D.25.在边长为2的正方形ABCD内部任取一点M,则满足的概率为()A.B.C.D.6.如图所示,已知||=1,||=,=0,点C在线段AB上,且∠AOC=30°,设=m+n(m,n∈R),则m﹣n等于()A.B.C.﹣D.﹣7.如图所示是一个几何体的三视图,则这个几何体的表面积是()(7题)(8题)A.3+B.2+C.2+D.3+8.若[x]表示不超过x的最大整数,执行如图所示的程序框图,则输出S的值为()A.3B.5C.7D.109.已知函数f(x)=cos(x+)sinx,则函数f(x)的图象()A.最小正周期为T=2πB.关于点(,﹣)对称C.在区间(0,)上为减函数D.关于直线x=对称10.已知抛物线y2=2px(p>0),若定点(2p,1)与直线kx+y+2k+2=0距离的最大值是5,则p的值为()A.1B.2C.3D.411.如图,在菱形ABCD中,∠BAD=60°,AB=2,E为对角线BD的中点,将△ABD沿BD折起到△PBD的位置,若∠PEC=120°,则三棱锥P﹣BCD的外接球的表面积为()A.28πB.32πC.16πD.12π12.定义在R上的函数f(x)满足,f(0)=e+2(其中e为自然对数的底数),则不等式的解集为()A.(﹣∞,0)B.(﹣∞,e+2)C.(﹣∞,0)∪(e+2,+∞)D.(0,+∞)二、填空题(本大题共4小题,每小题5分,共20分。把答案填在题中横线上)13.若a、b满足条件3+log2a=2﹣log2b(a>0,b>0),则的最小值为____.14.已知为圆O:的两条互相垂直的弦,且垂足为,则四边形ABCD的面积的最大值为______.15.不等式ex≥kx对任意实数x恒成立,则实数k的最大值为_____.16.若函数f(x)=x3+2x2+x+a的零点成等差数列,则a=______.三、解答题(解答应写出文字说明,证明过程或演算步骤)17.(本小题满分12分)Sn为数列{an}的前n项和,Sn=2an﹣2(n∈N+)(1)求{an}的通项公式;(2)若bn=3nan,求数列{bn}的前n项和Tn.18.(本小题满分12分)某校在高三抽取了500名学生,记录了他们选修A、B、C三门课的选修情况,如表:科目学生人数ABC120是否是60否否是70是是否50是是是150否是是50是否否(Ⅰ)试估计该校高三学生在A、B、C三门选修课中同时选修2门课的概率.(Ⅱ)若该高三某学生已选修A,则该学生同时选修B、C中哪门的可能性大?19.(本小题满分12分)如图,已知在多面体ABCDEF中,ABCD为正方形,EF∥平面ABCD,M为FC的中点,AB=2,EF到平面ABCD的距离为2,FC=2.(1)证明:AF∥平面MBD;(2)若EF=1,求VF﹣MBE.20.(本小题满分12分)已知椭圆C:(a>b>0)的焦距为,且椭圆C过点A(1,),(Ⅰ)求椭圆C的方程;(Ⅱ)若O是坐标原点,不经过原点的直线L:y=kx+m与椭圆交于两不同点P(x1,y1),Q(x2,y2),且y1y2=k2x1x2,求直线L的斜率k;(Ⅲ)在(Ⅱ)的条件下,求△OPQ面积的最大值.21.(本小题满分12分)已知函数.(Ⅰ)当0<a≤1时,求函数f(x)的单调区间;(Ⅱ)是否存在实数a,使f(x)≤x恒成立,若存在,求出实数a的取值范围;若不存在,说明理由.请考生在第22、23题中任选一题作答,如果多做,则按所做的第一题计分,作答时请写清题号。22.(本小题满分10分)选修4-4:坐标系与参数方程以直角坐标系的原点O为极点,轴的正半轴为极轴,且两个坐标系取相等的单位长度.已知过点P(1,1)的直线的参数方程是(I)写出直线的极坐标方程;(II)设与圆相交于两点A、B,求点P到A、B两点的距离之积23.(本小题满分10分)选修4-5:不等式选讲已知函数()|1||3|fxxx.(Ⅰ)求的取值范围,使()fx为常函数;(Ⅱ)若关于的不等式()0fxa有解,求实数的取值范围.文科试题答案及解析1.解:由x2<4,解得﹣2<x<2.∴B=(﹣2,2),又集合A={x|0<x≤3}=(0,3],∴A∪B=(﹣2...