3.2.1直线的点斜式方程VIP免费

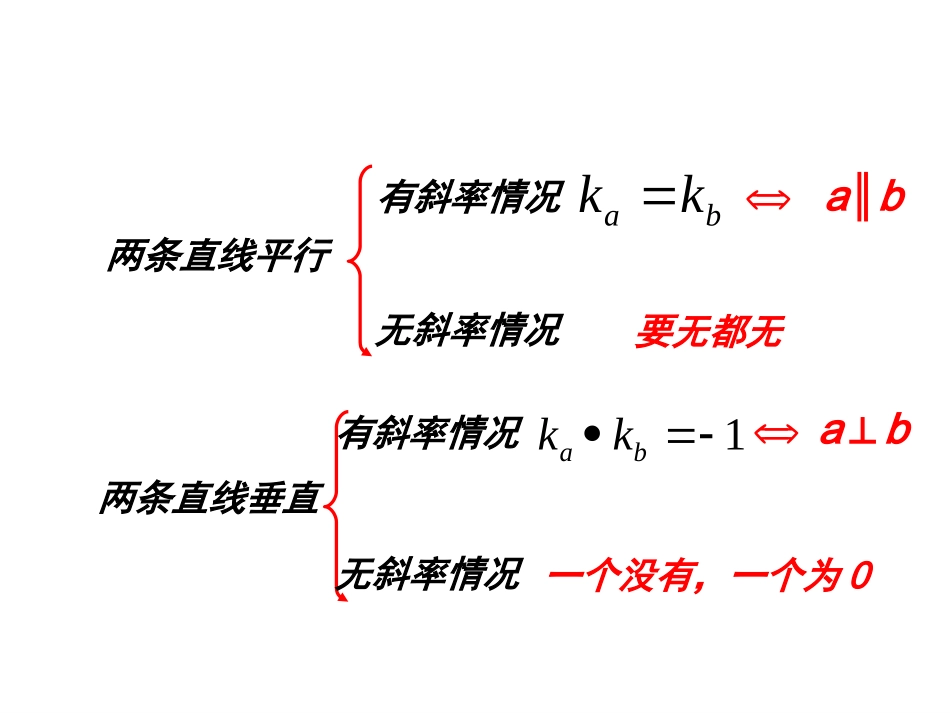
3.2.1直线的点斜式方程两条直线平行有斜率情况无斜率情况bakkab∥要无都无两条直线垂直有斜率情况无斜率情况1bakkab⊥一个没有，一个为0如果以一个方程的解为坐标的点都上某条直线上的点，反过来，这条直线上的点的坐标都是这个方程的解，那么，这个方程就叫做这条直线的方程，这条直线就叫做这个方程的直线.直线方程的概念新课讲授新课讲授已知直线l经过已知点P1（x1，y1），并且它的斜率是k，求直线l的方程。lOxy.P1根据经过两点的直线斜率公式，得11xxkyy可化为11xxyyk由由直线上一点直线上一点和和直线的斜率直线的斜率确定的直线方程，叫确定的直线方程，叫直线的直线的点斜式方程点斜式方程。。P.1、直线的点斜式方程：设点P（x，y）是直线l上不同于P1的任意一点。1、直线的点斜式方程：(1)、当直线l的倾斜角是00时，tan00=0,即k=0，这时直线l与x轴平行或重合l的方程：y-y1=0或y=y1(2)、当直线l的倾斜角是900时，直线l没有斜率，这时直线l与y轴平行或重合l的方程：x-x1=0或x=x1Oxyx1lOxyy1l点斜式方程的应用：例1：一条直线经过点P1（-2，3），倾斜角α=450，求这条直线的方程，并画出图形。解：这条直线经过点P1（-2，3）,斜率是k=tan450=1代入点斜式得y－3=x+2Oxy-55°P1°°1、写出下列直线的点斜式方程：练习2),1,3()1(斜率是经过A030),2,2()2(倾斜角是经过B2、说出下列点斜式方程所对应的直线斜率和倾斜角：(1)y-2=x-1332)2(xy00),5,0()3(倾斜角是经过COxy.(0,b)2、直线的斜截式方程：已知直线l的斜率是k，与y轴的交点是P（0，b），求直线方程。代入点斜式方程，得l的直线方程：y-b=k（x-0）即y=kx+b。(2)直线l与y轴交点(0,b)的纵坐标b叫做直线l在y轴上的截距。方程(2)是由直线的斜率k与它在y轴上的截距b确定，所以方程(2)叫做直线的斜截式方程，简称斜截式。斜截式方程的应用：例2：斜率是5，在y轴上的截距是4的直线方程。解：由已知得k=5，b=4，代入斜截式方程y=5x+4斜截式方程:y=kx+b几何意义：k是直线的斜率，b是直线在y轴上的截距练习3、写出下列直线的斜截式方程：2,23)1(轴上的截距是在斜率是y4,2)2(轴上的截距是在斜率是y练习4、已知直线l过A（3，-5）和B（-2，5），求直线l的方程解：∵直线l过点A（3，-5）和B（-2，5）23255lk将A（3，-5），k=-2代入点斜式，得y－(－5)=－2(x－3)即2x+y－1=0例题分析：?l(2)?l)1(::,:32121222111的条件是什么的条件是什么试讨论已知直线例llbxkylbxkyl∥1l,l2121212121kklbbkkl且∥222111:,:bxkylbxkyl练习判断下列各直线是否平行或垂直(1)(2)11:32lyx21:22lyx15:3lyx23:5lyx①直线的点斜式，斜截式方程在直线斜率存在时才可以应用。②直线方程的最后形式应表示成二元一次方程的一般形式。练习5、求过点（1，2）且与两坐标轴组成一等腰直角三角形的直线方程。解：∵直线与坐标轴组成一等腰直角三角形∴k=±1直线过点（1，2）代入点斜式方程得y-2=x-1或y－２＝－（ｘ－１）即ｘ－ｙ＋１＝0或ｘ＋ｙ－１＝0