24.4弧长和扇形面积(通用)VIP免费

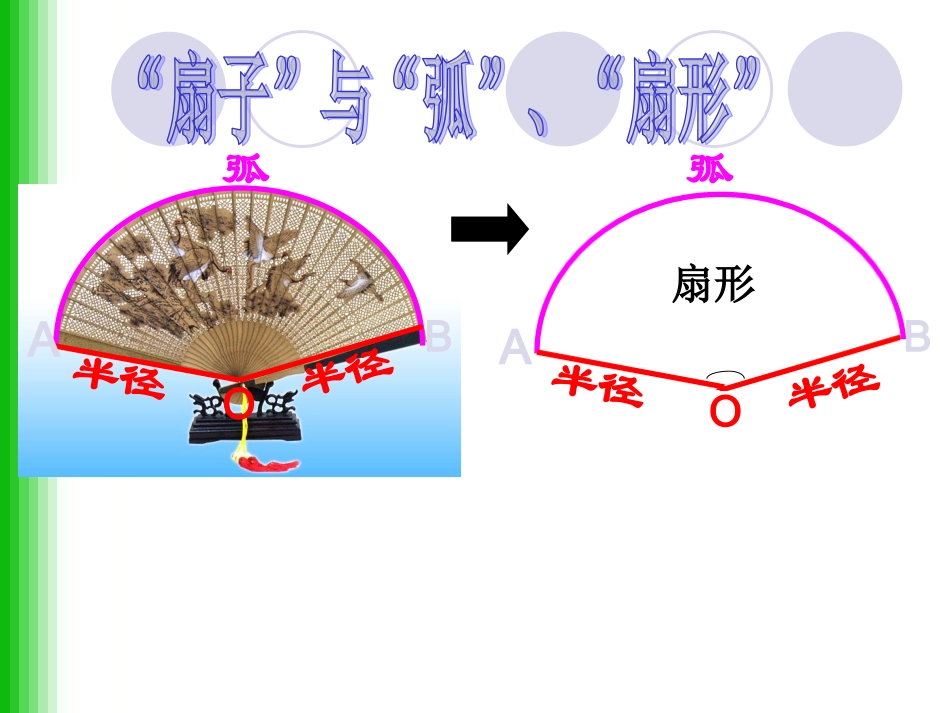
教学目标1.探索及推导弧长计算公式和扇形面积公式，能够从公式来源的角度上加以理解；2.熟练应用公式并能解决相关的实际问题；3.理解并把握课程中涵盖的数学思想和数学方法并加以应用；重点：两个公式的推导；难点：两个公式的推导及实际运用.弧弧半径半径半径半径AABBOO扇形观察：制造弯形管道时，经常要先按中心线计算“展直长度”(图中虚线的长度)，再下料，这就涉及到计算弧长的问题认真阅读课本第111页的内容，完成下面的练习并体验知识点的形成过程.知识点一弧长的计算思考:（1）圆的周长公式_________（2）圆的周长可以看作___度的圆心角所对的弧．（3）1°的圆心角所对的弧长是_______2°的圆心角所对的弧长是_______360180r2180rC=2πR180Rnln°ABO若设⊙O半径为R，n°的圆心角所对的弧长为，则l3°的圆心角所对的弧长是.……n°的圆心角所对的弧长是.3180r180nr1.已知弧所对的圆心角为900，半径是4，则弧长为______2.已知一条弧的半径为9，弧长为8π，那么这条弧所对的圆心角为____。3.钟表的轴心到分针针端的长为5cm,那么经过40分钟,分针针端转过的弧长是()A.B.C.D.cm310cm320cm325cm3502160°B小结：弧长公式涉及三个量:1,弧长,2,圆心角的度数,3,弧所在的半径，知道其中两个量，就可以求第三个量。弧长你会算了吗？应用：制造弯形管道时，要先按中心线计算“展直长度”，再下料，试计算图所示管道的展直长度L(结果取整数)解：由题知，R=900mm,n=100,则由弧长公式，可得弧AB的长l（mm）1570500180900100因此所要求的展直长度L（mm）297015707002答：管道的展直长度为2970mm．如下图，由组成圆心角的两条半径和圆心角所对的弧围成的图形是扇形。半径半径圆心角圆心角弧ABOBA扇形知识点二扇形面积的计算那么：在半径为R的圆中,n°的圆心角所对的扇形面积的计算公式为360Rn2扇形S2R3602R36036022RnRn360°(1)如果圆的半径为R，则圆的面积为多少？(2)圆的面积可以看成多少度圆心角扇形的面积？(3)l°的圆心角对应的扇形面积为多少？(4)n°的圆心角对应的扇形面积为多少？2°的圆心角对应的扇形面积为多少？3°的圆心角对应的扇形面积为多少？36022R36032R知识点二扇形面积的计算比较扇形面积与弧长公式,用弧长表示扇形面积:ABOO知识之间想一想：扇形的面积公式与什么公式类似？180Rnl3602RnS扇形lRS21扇形2.2.已知扇形的圆心角为已知扇形的圆心角为303000，面积为，则这，面积为，则这个扇形的半径个扇形的半径R=____R=____．．23cm11..已知扇形的圆心角为已知扇形的圆心角为120°120°，半径为，半径为22，则这个扇，则这个扇形的面积为形的面积为_______._______.436cm6cm做一做：做一做：小结：扇形面积公式涉及三个量扇形面积,圆心角的度数,弧所在的半径，知道其中两个量，就可以求第三个量。综合应用0BACD例2.如图、水平放置的圆柱形排水管道的截面半径是0.6m，其中水面高0.3m，求截面上有水部分的面积。（结果保留小数点后两位）有水部分面积：S弓形=S扇形-S△解：如图，连接OA,OB,作OC⊥AB,垂足为D,交弧AB于点C,连接AC. OC=0.6m，DC=0.3m∴OD=OC-DC=0.3m∴OD=DC AD⊥OC∴AD是线段OC的垂直平分线∴AC=AO=OC∴△AOC是等边三角形∴∠AOD=60〬)(22.03.036.02112.0213600.612022mODABSSSOABOAB扇形∴有水部分的面积约是0.22m2∴∠AOB=2∠AOD=120〬∴有水部分的面积是：在Rt△OAD中，AD==0.322ODOA3∴AB=36.0练习：如图、水平放置的圆柱形排水管道的截面半径是0.6cm，其中水面高0.9cm，求截面上有水部分的面积。0ABDCE变式训练变式训练S弓形=S扇形+S△感悟：①当弓形面积小于半圆时S弓形=S扇形-S△②当弓形面积大于半圆时S弓形=S扇形+S△回顾与归纳（一）回顾与归纳（一）180Rnl2nRS360扇形1lR21.弧长公式：2.扇形面积公式：注意：两个公式的联系和区别3.学会几何建模，既把实际问题转化为几何问题（把实际问题中的条件和结论与数学问题中的条件和结论对应起来是解题之关键）回顾与归纳（二）回顾与归纳（二）组合图形的面积：（1）割...