三角形中的角平分线VIP免费

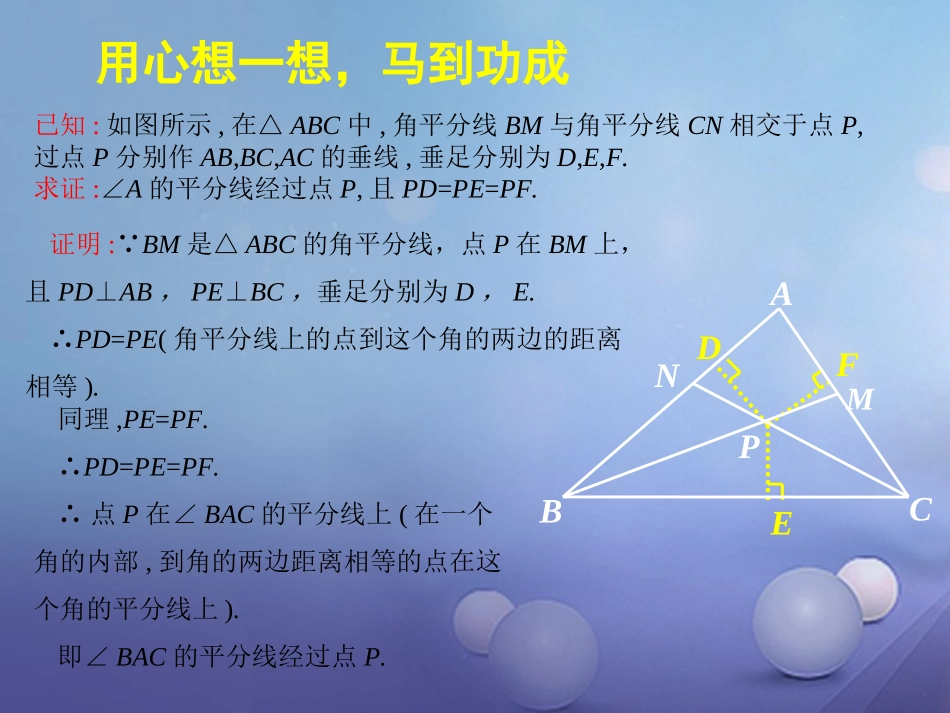
三角形三边的垂直平分线交于一点，那三角形的三个内角的角平分线交于一点吗?用心想一想，马到功成发现：三角形的三个内角的角平分线交于一点．这一点到三角形三边的距离相等．用心想一想，马到功成DEFMNCBAP已知:如图所示,在△ABC中,角平分线BM与角平分线CN相交于点P,过点P分别作AB,BC,AC的垂线,垂足分别为D,E,F.求证:∠A的平分线经过点P,且PD=PE=PF.证明:∵BM是△ABC的角平分线，点P在BM上，且PD⊥AB，PE⊥BC，垂足分别为D，E.∴PD=PE(角平分线上的点到这个角的两边的距离相等).同理,PE=PF.∴PD=PE=PF.∴点P在∠BAC的平分线上(在一个角的内部,到角的两边距离相等的点在这个角的平分线上).即∠BAC的平分线经过点P.定理：三角形的三条角平分线相交于一点，并且这一点到三条边的距离相等．三角形角平分线的性质定理比较三角形三边的垂直平分线和三条角平分线的性质定理三边垂直平分线三条角平分线三角形锐角三角形交于三角形内一点交于三角形内一点钝角三角形交于三角形外一点直角三角形交于斜边的中点交点性质到三角形三个顶点的距离相等到三角形三边的距离相等例：如图所示,在△ABC中,AC=BC,∠C=90°,AD是△ABC的角平分线,DE⊥AB,垂足为E.(1)已知CD=4cm,求AC的长;(2)求证AB=AC+CD.解:(1)∵AD是△ABC的角平分线,DC⊥AC,DE⊥AB,垂足为E,∴DE=CD=4cm(角平分线上的点到这个角的两边的距离相等).∵AC=BC,∴∠B=∠BAC(等边对等角).∵∠C=90°,∴∠B=×90°=45°.∴∠BDE=90°-45°=45°.∴BE=DE(等角对等边).122242DE2在等腰直角三角形BDE中,BD=cm,∴AC=BC=CD+BD=(4+4)cm.课堂小结,畅谈收获：本节课我们利用角平分线的性质和判定定理证明了三角形三条角平分线交于一点，且这一点到三角形各边的距离相等．并综合运用我们前面学过的性质定理等解决了几何中的计算和证明问题．课内拓展延伸如图，△ABC中，点O是∠BAC与∠ABC的平分线的交点，过O作与BC平行的直线分别交AB、AC于D、E．已知△ABC的周长为15，BC的长为6，求△ADE的周长.CBAEDO