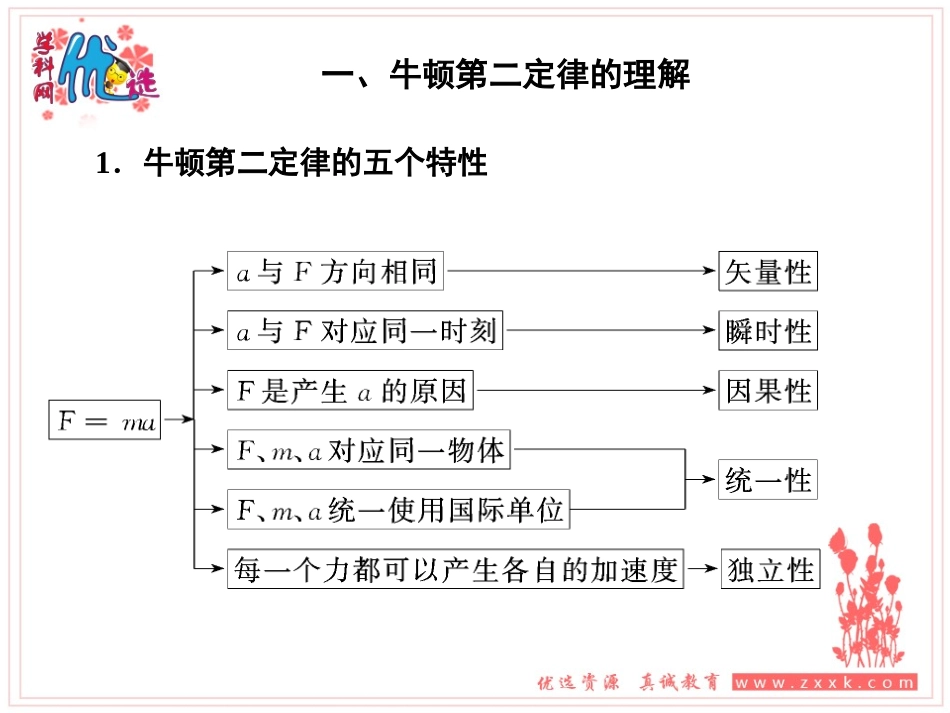
第11讲牛顿第二定律★重难点一:牛顿第二定律的理解★一、牛顿第二定律的理解1.牛顿第二定律的五个特性2.合力、加速度、速度间的决定关系(1)不管速度是大是小,或是零,只要合力不为零,物体都有加速度。(2)a=ΔvΔt是加速度的定义式,a与Δv、Δt无必然联系;a=Fm是加速度的决定式,a∝F,a∝1m。(3)合力与速度同向时,物体加速运动;合力与速度反向时,物体减速运动。二、牛顿第二定律瞬时性分析1.两种模型:牛顿第二定律的表达式为F=ma,其核心是加速度与合外力的瞬时对应关系,二者总是同时产生、同时消失、同时变化,具体可简化为以下两种模型:(1)刚性绳(或接触面)——不发生明显形变就能产生弹力的物体,剪断(或脱离)后,其弹力立即消失,不需要形变恢复时间。(2)弹簧(或橡皮绳)——两端同时连接(或附着)有物体的弹簧(或橡皮绳),特点是形变量大,其形变恢复需要较长时间,在瞬时性问题中,其弹力的大小往往可以看成保持不变。2.解题思路:分析瞬时变化前后物体的受力情况―→列牛顿第二定律方程―→求瞬时加速度在求解瞬时加速度时应注意的两个问题(1)物体的受力情况和运动情况是时刻对应的,当外界因素发生变化时,需要重新进行受力分析和运动分析。(2)加速度可以随着力的突变而突变,而速度的变化需要一个过程的积累,不会发生突变。【特别提醒】轻绳、轻杆和轻弹簧三种模型的异同1.三个模型的相同点:(1)“轻”——质量和重力均不计.(2)在任何情况下,绳中张力相等,绳、杆和弹簧两端受到的弹力也相等.【特别提醒】轻绳、轻杆和轻弹簧三种模型的异同2.三个模型的不同点:(1)施力和受力特点轻绳——只能产生沿绳方向的拉力.轻杆——不仅可以产生和承受沿杆方向的拉力和压力,还可以产生和承受不沿杆方向的拉力和压力.轻弹簧——可以产生和承受沿弹簧伸缩方向的拉力和压力.【特别提醒】轻绳、轻杆和轻弹簧三种模型的异同2.三个模型的不同点:(2)力的变化特点①轻绳——拉力的产生、变化或消失不需要时间,具有突变性和瞬时性.②轻杆——拉力和压力的产生、变化或消失不需要时间,具有突变性和瞬时性.③轻弹簧——弹力的产生、变化或消失需要时间,不具有突变性,即只能渐变,但具有瞬时性,即不同形变的瞬间,对应不同的弹力.(注意:当轻弹簧的自由端无重物时,形变消失不需要时间,即具有突变性)【特别提醒】【典型例题】(多选)如图所示,A、B球的质量相等,弹簧的质量不计,倾角为θ的斜面光滑,系统静止时,弹簧与细线均平行于斜面,在细线被烧断的瞬间,下列说法正确的是:()A.两个小球的瞬时加速度均沿斜面向下,大小均为gsinθB.B球的受力情况未变,瞬时加速度为零C.A球的瞬时加速度沿斜面向下,大小为2gsinθD.弹簧有收缩的趋势,B球的瞬时加速度向上,A球的瞬时加速度向下,瞬时加速度都不为零【解析】设弹簧的弹力大小为F,由平衡条件可知,F=mgsinθ,烧断细线之后瞬间,弹簧弹力不变,故B球受力情况不变,加速度为0,B正确,A、D均错误;以A为研究对象,由牛顿第二定律可得:F+mgsinθ=maA,解得:aA=2gsinθ,故C正确。【答案】BC★重难点二:动力学的两类基本问题★1.解决两类基本问题的方法以加速度为“桥梁”,由运动学公式和牛顿第二定律列方程求解,具体逻辑关系如图:2.两类动力学问题的解题步骤解决两类动力学问题的两个关键点【特别提醒】【典型例题】一质量为m=2kg的滑块能在倾角为θ=30°的足够长的斜面上以a=2.5m/s2匀加速下滑。如图所示,若用一水平向右恒力F作用于滑块,使之由静止开始在t=2s内能沿斜面运动位移x=4m。求:(g取10m/s2)(1)滑块和斜面之间的动摩擦因数μ;(2)恒力F的大小。【解析】(1)根据牛顿第二定律可得:mgsin30°-μmgcos30°=ma解得:μ=36。(2)使滑块沿斜面做匀加速直线运动,有加速度向上和向下两种可能。当加速度沿斜面向上时,Fcos30°-mgsin30°-μ(Fsin30°+mgcos30°)=ma1,根据题意可得a1=2m/s2,代入数据得:F=7635N当加速度沿斜面向下时:mgsin30°-Fcos30°-μ(Fsin30°+mgcos30°)=ma1代入数据得:F=437N。【答案】(1)36(2)7635N或437N★重难点三:动力学的图象问题★1....