探究与发现祖暅原理与柱体、椎体、球体的体积-(2)VIP免费

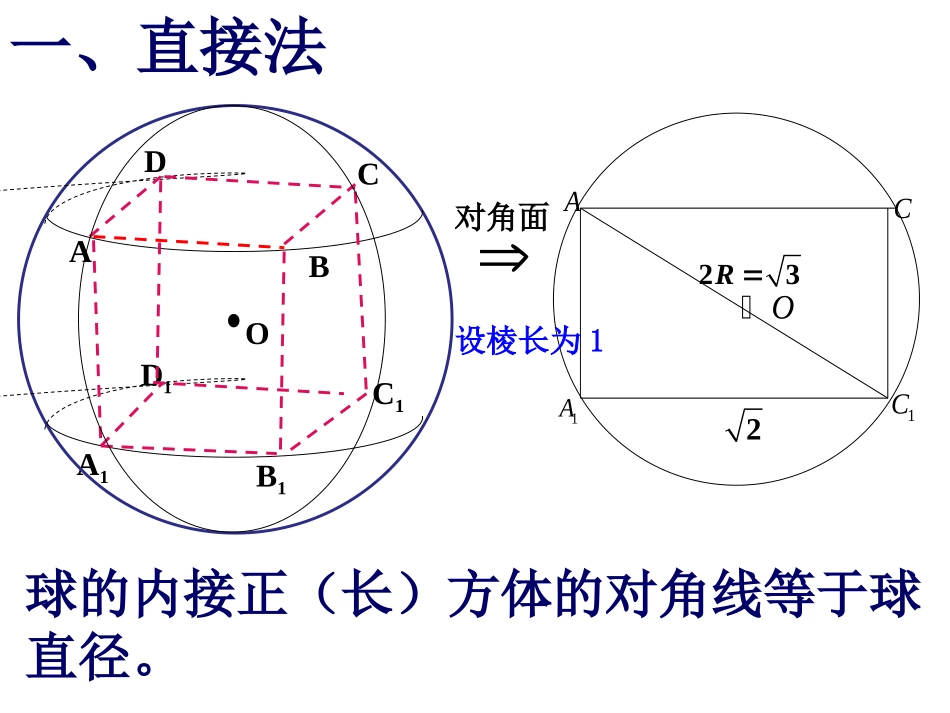
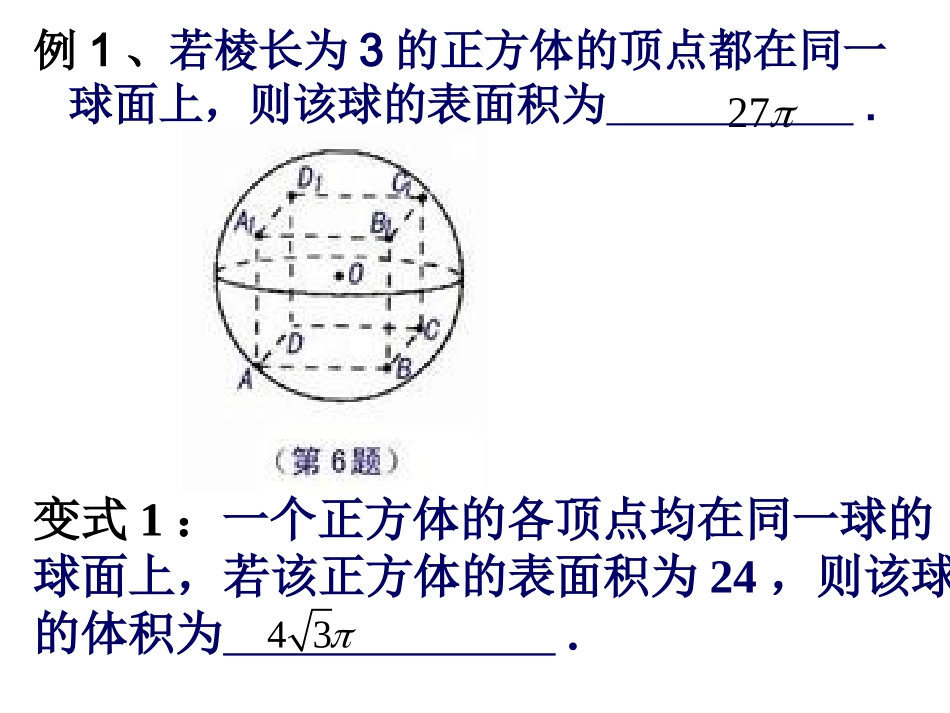
球的内接正（长）方体的对角线等于球直径。一、直接法ABCDD1C1A1OB1A1AC1CO对角面223R设棱长为127变式1：一个正方体的各顶点均在同一球的球面上，若该正方体的表面积为24，则该球的体积为.43例1、若棱长为3的正方体的顶点都在同一球面上，则该球的表面积为.变式2：一个长方体的各顶点均在同一球面上，且一个顶点上的三条棱长分别为1,2,3，则此球的表面积为.14变式3：已知各顶点都在一个球面上的正四棱柱高为4，体积为16，则这个球的表面积为（）A.B.C.D.16202432C.ra一、直接法内切球的直径等于正方体的棱长。一、直接法内切球的直径等于正方体的面对角线长。球内切于正方体的各条棱甲图乙图丙图例1甲球内切于正方体的各面，乙球内切于该正方体的各条棱，丙球外接于该正方体，则三球表面面积之比为()A.1:2:3B.C.D.1:2:31:8:27331:4:9球的外切正方体的棱长等于球直径。214=SR甲正方形的对角线等于球的直径。224=2SR乙球的内接正方体的对角线等于球直径。234=3SR丙AACBPO二、构造法例1、（2012辽宁16）已知正三棱锥P-ABC，点P,A,B,C都在半径为的球面上，若PA,PB,PC两两互相垂直，则球心到截面ABC的距离为。3331、构造正方体变式题、已知球O的面上四点A、B、C、D，则球O的体积为。3,BCABDABCABABCDA，平面29例5、求棱长为a的正四面体P–ABC的外接球的表面积。求正多面体外接球的半径求正方体外接球的半径变式题：一个四面体的所有棱长都为，四个顶点在同一球面上，则此球的表面积（）A.B.C.D.234336A2、构造长方体已知点A、B、C、D在同一个球面上，，则B、C两点间的球面距离是().BBCDA平面BCDC6,AC=213,AD=8AB34，，变式、(2013郑州质检)在三棱锥中，,则该三棱锥的内接球的表面积为。ABCD6,5ABCDACBDADBC43三、确定球心位置法例、在矩形ABCD中，AB=4，BC=3，AC沿将矩形ABCD折成一个直二面角B-AC-D，则四面体ABCD的外接球的体积为()12125.A9125.B6125.C3125.DCAODB图4Ｃ四、公式法例、一个六棱柱的底面是正六边形，其侧棱垂直于底面，已知该六棱柱的顶点都在同一个球面上，且该六棱柱的体积为，底面周长为３，则这个球的体积为。8934思考题：半径为R的球的外切圆柱(球与圆柱的侧面、两底面都相切)的表面积为____，体积____．26R32R.86463434,463332,32311,33,,3322212121111RVRRRAOORtAOSASOrABCrAORSOOABCDSSO球，解得中，由勾股定理得，在从而识得，中，用解直角三角形知则在上，设外接球半径为在的高，外接球的球心是正四面体解：设五、构造直角三角形例13、求棱长为1的正四面体外接球的体积。六、寻求轴截面圆半径法例1、正四棱锥S-ABCD的底面边长和各侧棱长都为，点S,A,B,C,D都在同一球面上，则此球的体积为.CDABSO1图3解设正四棱锥的底面中心为，外接球的球心为O，如图3所示.∴由球的截面的性质，可得又，∴球心O必在所在的直线上.∴的外接圆就是外接球的一个轴截面圆，外接圆的半径就是外接球的半径.在中，由是外接圆的半径，也是外接球的半径.故1OABCDOO平面11SOASCASC12..,2,2222ACRtACASCACSCSAACSCSA为斜边的是以得34球VABCDSO平面12几何体的内切球例、正四面体的棱长为a，则其内切球和外接球的半径是多少？图1解：如图1所示，设点o是内切球的球心，正四面体棱长为a．由图形的对称性知，点o也是外接球的球心．设内切球半径为r，外接球半径为R．正四面体的表面积正四面体的体积在中，即，得得223434aaS表22221234331BEABaAEaVBCDA322212233123aaaaBCDAVrS表31aaaSVrBCDA12631223323表BEORt222EOBEBO22233raRaR46rR32013辽宁102011辽宁12