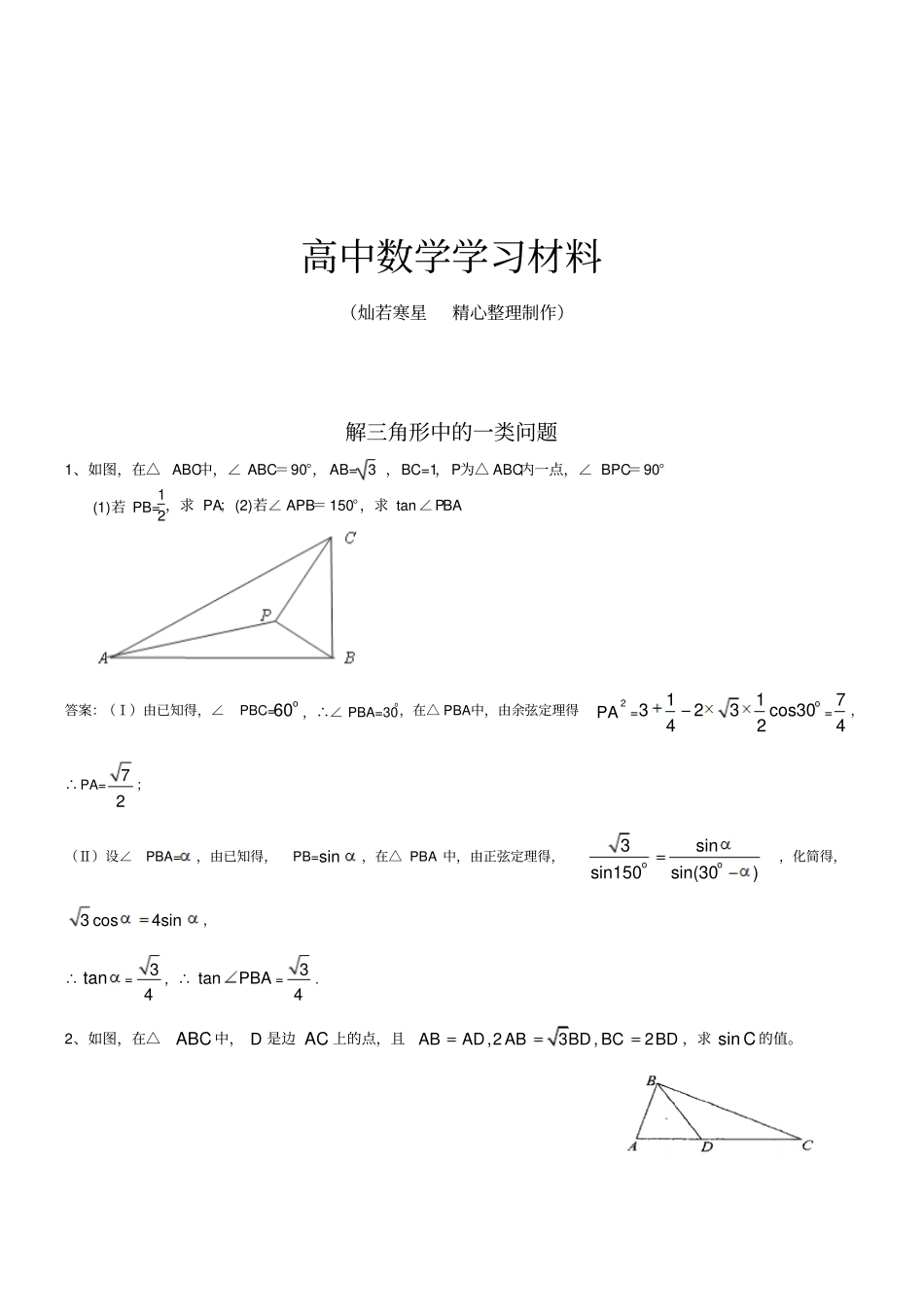
高中数学学习材料(灿若寒星精心整理制作)解三角形中的一类问题1、如图,在△ABC中,∠ABC=90°,AB=3,BC=1,P为△ABC内一点,∠BPC=90°(1)若PB=12,求PA;(2)若∠APB=150°,求tan∠PBA答案:(Ⅰ)由已知得,∠PBC=o60,∴∠PBA=30o,在△PBA中,由余弦定理得2PA=o11323cos3042=74,∴PA=72;(Ⅱ)设∠PBA=,由已知得,PB=sin,在△PBA中,由正弦定理得,oo3sinsin150sin(30),化简得,3cos4sin,∴tan=34,∴tanPBA=34.2、如图,在△ABC中,D是边AC上的点,且,23,2ABADABBDBCBD,求sinC的值。3、如图,△ABC中,AB=AC=2,BC=23,点D在BC边上,∠ADC=45°。(1)求AD的长度;(2)求BD:DC的值。答案(1)2;(2)4、ABC中,D为边BC上的一点,33BD,5sin13B,3cos5ADC,求AD.5、在△ABC中,D为边BC上一点,BD=12DC,ADB=120°,AD=2,若△ADC的面积为33,求BAC。答案:606、ABC中,090C,M是BC的中点,若31sinBAM,求sinBAC。【答案】637、如图ABC中,已知点D在BC边上,ADAC,22sin,32,33BACABAD,求BD的长。【答案】3