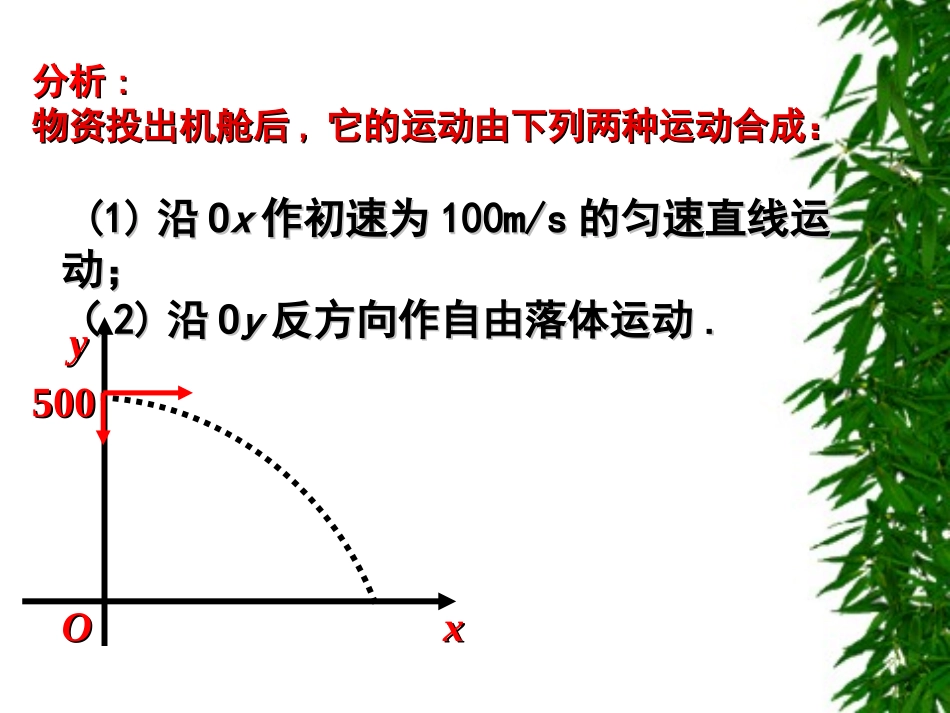
如图如图,,一架救援飞机在离灾区地面一架救援飞机在离灾区地面500m500m高处以高处以100m/s100m/s的速度作水平直线飞行的速度作水平直线飞行..为使投放救援为使投放救援物资准确落于灾区指定的地面物资准确落于灾区指定的地面((不记空气阻力不记空气阻力),),飞行员应如何确定投放时机呢?飞行员应如何确定投放时机呢?友情提示:友情提示:即求飞行员在离救援即求飞行员在离救援点的水平距离多远时,点的水平距离多远时,开始投放物资?开始投放物资??救援点投放点探究探究xxyy500500OO分析分析::物资投出机舱后物资投出机舱后,,它的运动由下列两种运动合成:它的运动由下列两种运动合成:(1)(1)沿沿OOxx作初速为作初速为100m/s100m/s的匀速直线运的匀速直线运动;动;((2)2)沿沿OOyy反方向作自由落体运动反方向作自由落体运动..xy500o0,y令10.10.ts得100,1010.xtxm代入得.1010所m以,飞行员在离救援点的水平距离约为时投放物资,可以使其准确落在指定位置txy解:建立如图所示坐标系,物资出舱后,设在时刻,水平位移为,垂直高度为,所以2100,1500.2xtygt)2(g=9.8m/s(),().xftygt(1)且对于且对于tt的每一个允许值的每一个允许值,,由方程组由方程组(1)(1)所确所确定的点定的点M(M(x,yx,y))都在这条曲线上都在这条曲线上,,则方程则方程(1)(1)就就叫做这条曲线的参数方程叫做这条曲线的参数方程,,联系变数联系变数x,yx,y的的变数变数tt叫做参变数叫做参变数,,简称参数简称参数..相对于参数方程而言,直接给出点的相对于参数方程而言,直接给出点的坐标间关系的方程叫做普通方程。坐标间关系的方程叫做普通方程。11、参数方程的概念:、参数方程的概念:一般地一般地,,在平面直角坐标系中在平面直角坐标系中,,如果曲如果曲线上任意一点的坐标线上任意一点的坐标xx,,yy都是某个变数都是某个变数tt的函数的函数关于参数几点说明:关于参数几点说明:参数是联系变数参数是联系变数x,yx,y的桥梁的桥梁,,1.1.参数方程中参数可以是有物理意义参数方程中参数可以是有物理意义,,几何意义几何意义,,也可以没有明显意义;也可以没有明显意义;2.2.同一曲线选取参数不同同一曲线选取参数不同,,曲线参数方程曲线参数方程形式也不一样形式也不一样;;3.3.在实际问题中要确定参数的取值范围在实际问题中要确定参数的取值范围;;例例1:1:已知曲线已知曲线CC的参数方程是的参数方程是((11)判断点)判断点MM11(0,1)(0,1),,MM22(5,4)(5,4)与曲线与曲线CC的位置关系;的位置关系;((22)已知点)已知点MM33(6,(6,aa))在曲线在曲线CC上上,,求求aa的值。的值。23,()21.xttyt为参数解:解:(1)(1)把点把点MM11的坐标的坐标(0,1)(0,1)代入方程组,解得代入方程组,解得t=0t=0,,所以所以MM11在曲线上.在曲线上.124352tt把点把点MM22的坐标的坐标(5,4)(5,4)代入方程组,得到代入方程组,得到12362tat(2)(2)因为点因为点MM33(6,a)(6,a)在曲线在曲线CC上,所以上,所以解得解得t=2,a=9t=2,a=9所以,所以,a=9.a=9.这个方程组无解,因此点MM22不在曲线上练习:练习:已知曲线已知曲线CC的参数方程的参数方程且点且点M(5,4)M(5,4)在该曲线上在该曲线上..((11)求常数)求常数a;a;((22)求曲线)求曲线CC的普通方程的普通方程..212,().xttyat为参数,aR解解::(1)(1)由题意可知由题意可知::1+2t=51+2t=5atat22=4=4解得解得::a=1a=1t=2t=2∴∴a=1a=1(2)(2)由已知及由已知及(1)(1)可得可得,,曲线曲线CC的方程的方程为为::xx=1+2t=1+2tyy=t=t22由第一个方程得由第一个方程得::12xt代入第二个方程得代入第二个方程得::21(),2xy故所求曲线的普通方程为(故所求曲线的普通方程为(xx-1)-1)22=4=4yy2、圆的参数方程圆的参数方程与普通方程的互化sincosryrxx2+y2=r2222)()(rbyaxsincosrbyrax注:1、参数方程的特点是没有直接体现曲线上点的横、纵坐标之间的关系,而是分别体现了点的横、纵坐标与参数之间的关系。2、参数方程的应用往往是在x与y直接关系很难或不可能体现时...