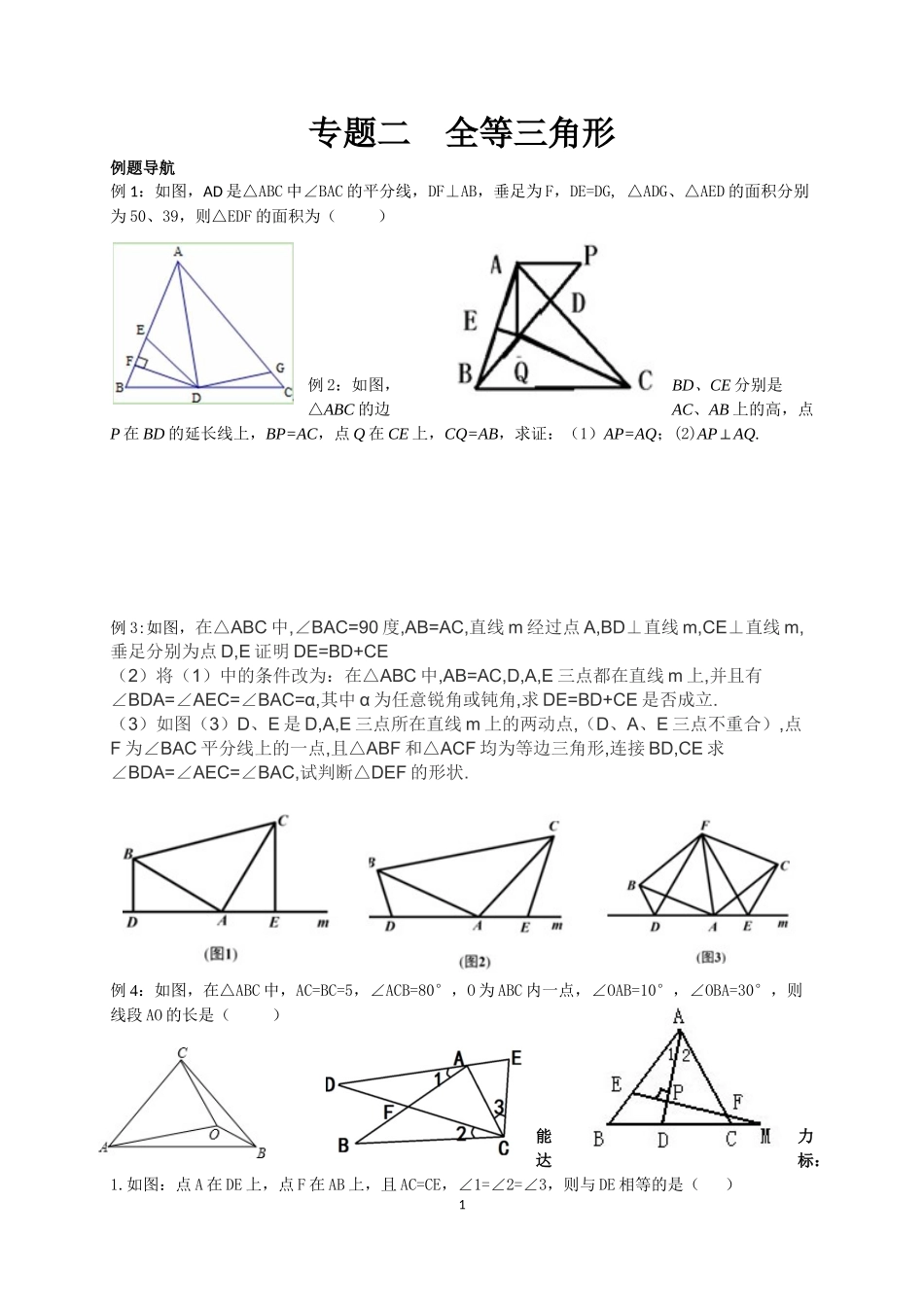
专题二全等三角形例题导航例1:如图,AD是△ABC中∠BAC的平分线,DF⊥AB,垂足为F,DE=DG,△ADG、△AED的面积分别为50、39,则△EDF的面积为()例2:如图,BD、CE分别是△ABC的边AC、AB上的高,点P在BD的延长线上,BP=AC,点Q在CE上,CQ=AB,求证:(1)AP=AQ;(2)AP⊥AQ.例3:如图,在△ABC中,∠BAC=90度,AB=AC,直线m经过点A,BD⊥直线m,CE⊥直线m,垂足分别为点D,E证明DE=BD+CE(2)将(1)中的条件改为:在△ABC中,AB=AC,D,A,E三点都在直线m上,并且有∠BDA=∠AEC=∠BAC=α,其中α为任意锐角或钝角,求DE=BD+CE是否成立.(3)如图(3)D、E是D,A,E三点所在直线m上的两动点,(D、A、E三点不重合),点F为∠BAC平分线上的一点,且△ABF和△ACF均为等边三角形,连接BD,CE求∠BDA=∠AEC=∠BAC,试判断△DEF的形状.例4:如图,在△ABC中,AC=BC=5,∠ACB=80°,O为ABC内一点,∠OAB=10°,∠OBA=30°,则线段AO的长是()能力达标:1.如图:点A在DE上,点F在AB上,且AC=CE,∠1=∠2=∠3,则与DE相等的是()12.如图:∠1=∠2,EF⊥AD于点P,交BC的延长线于点M,求证:∠M=12(∠ACB-∠B)3.在△ABC中,AB=AC,点D是直线BC上一点(不与B、C重合),以AD为一边在AD的右侧作△ADE,使AD=AE,∠DAE=∠BAC,连接CE.(1)如图1,当点D在线段BC上,如果∠BAC=90°,则∠BCE=度;(2)设∠BAC=α,∠BCE=β.①如图2,当点D在线段BC上移动,则α,β之间有怎样的数量关系?请说明理由;②当点D在直线BC上移动,则α,β之间有怎样的数量关系?请直接写出你的结论.4.在四边形ABCD中,对角线AC平分∠BAD,AB>AD,求证:AB-AD