27.1《图形的相似》课件.2.1.相似三角形判定2SSSVIP免费

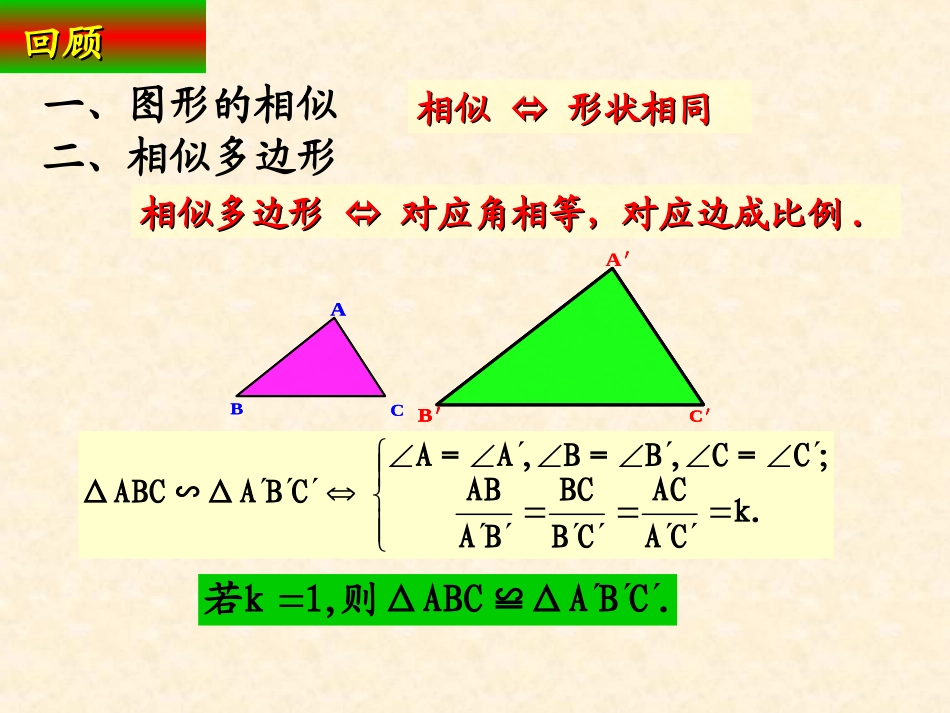
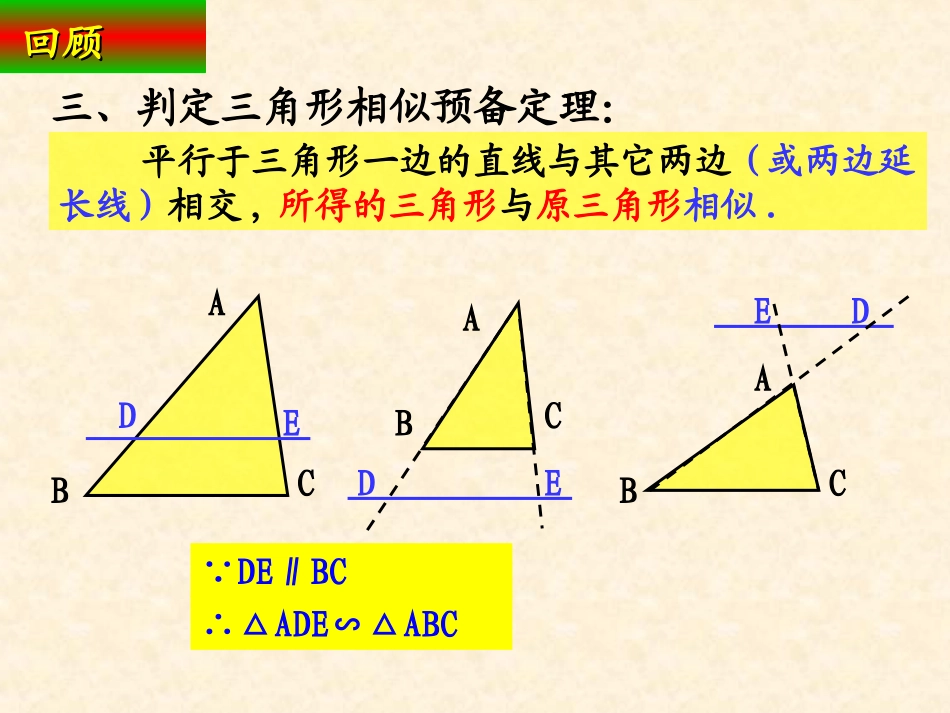
相似三角形判定相似三角形判定（（22））----定理定理(SSS)(SSS)九年级数学(下）相似2013年03回顾回顾一、图形的相似相似相似形状相同形状相同二、相似多边形相似多边形相似多边形对应角相等，对应边成比例对应角相等，对应边成比例..ABCABCA′B′C′A′B′C′B′C′k.CAACCBBCBAAB;CC＝,BB＝,AA＝CBAΔ∽ΔABC.CBAΔ≌则ΔABC1,若k平行于三角形一边的直线与其它两边(或两边延长线)相交,所得的三角形与原三角形相似.ABCDEABCDEABCDE∵DE∥BC∴△ADE∽△ABC三、判定三角形相似预备定理：回顾回顾问题问题11画△ABC,使AB=4cm,BC=5cm,AC=6cm;再画△A’B’C’,使A’B’=6cm,B’C’=7.5cm,A’C’=9cm.这两个三角形相似吗？为什么？ABCA’B’C’问题问题11ABCA’B’C’从而我们得出一个命题如果两个三角形的三组对应边的比相等,那么这两个三角形相似.ABCA’B’C’.CBAΔ∽求证：ΔABC.CAACCBBCBAAB中，CBA如图，在ΔABC和ΔDE证明:在△A´B´C´的边A´B´(或延长线)上截取A/D=AB,过点D作DE∥B´C´交A/C/于点E,则△A/DE∽△A/B/C/..CAEACBDEBADAAB,DA，CAACCBBCBAAB又,CAACCAEA,CBBCCBDEAC.EABC,DE∴△A/DE≅△ABC（SSS),∴△ABC∽△A/B/C/,三角形相似的判定定理1：三角形相似的判定定理1：如果两个三角形的三组对应边的比相等,那么这两个三角形相似.即：三边对应成比例,两三角形相似.ABCA’B’C’CBAΔ∽ΔABCkCAACCBBCBAAB例1试判定△ABC与A’B’C’是否相似，并说明理由．(1)AB=12cm，BC=15cm，AC＝24cmA’B’＝16cm，B’C’＝20cm，A’C’＝30cm，如图已知AEACDEBCADAB试说明∠BAD=∠CAE.ADCEBAEACDEBCADAB解∴ΔABC∽ΔADE∴∠BAC=∠DAE∴∠BAC-∠DAC=∠DAE-∠DAC即∠BAD=∠CAE例2检测一检测一(1)AB＝6cm，BC＝8cm，AC＝10cm，A’B’＝18cm，B’C’＝24cm，A’C’＝30cm．1.试判定△ABC与A’B’C’是否相似，并说明理由答案是2:1由。如果不相似，请说明理似比；吗？如果相似，求出相，它们相似CB和ΔACB有ΔA正方形网格上1cm3.如图在222111的边长为检测二检测二2、判断图中△AEB和△FEC是否相似？54303645EAFCB检测三检测三这节课你有什么收获？平行于三角形一边的直线与其它两边(或两边延长线)相交,所得的三角形与原三角形相似.三角形相似的判定预备定理：三角形相似的判定定理1：如果两个三角形的三组对应边的比相等,那么这两个三角形相似.即：三边对应成比例,两三角形相似.思考题:作业：作业：P541,2（1）、3（1）