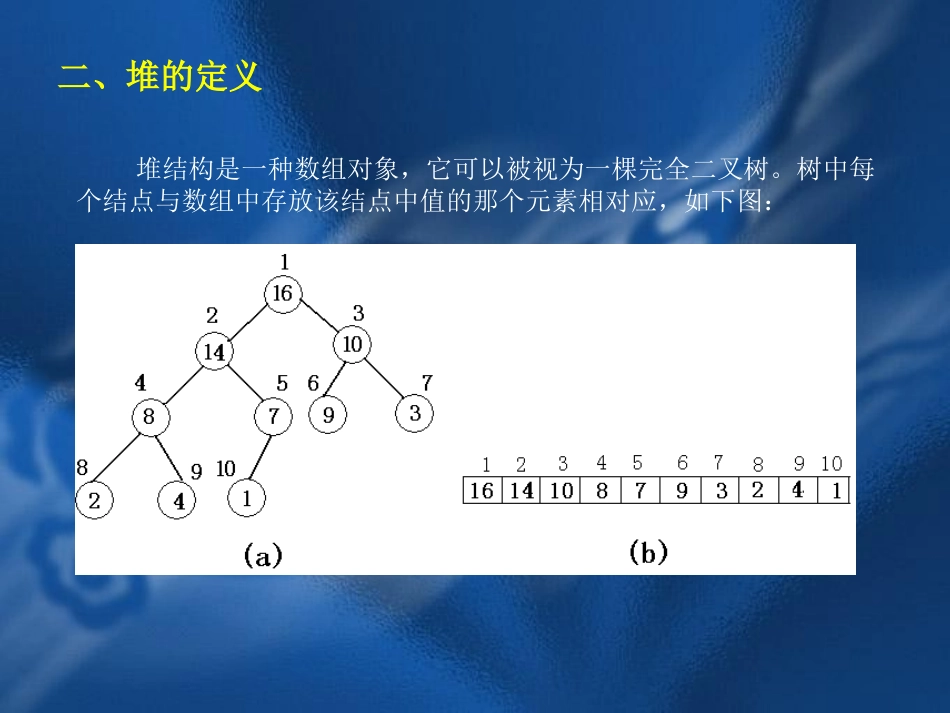
第三节堆及其应用一、预备知识完全二叉树:如果一棵深度为K二叉树,1至k-1层的结点都是满的,即满足2i-1,只有最下面的一层的结点数小于2i-1,并且最下面一层的结点都集中在该层最左边的若干位置,则此二叉树称为完全二叉树。二、堆的定义堆结构是一种数组对象,它可以被视为一棵完全二叉树。树中每个结点与数组中存放该结点中值的那个元素相对应,如下图:三、堆的性质设数组A的长度为len,二叉树的结点个数为size,size≤len,则A[i]存储二叉树中编号为i的结点值(1≤i≤size),而A[size]以后的元素并不属于相应的堆,树的根为A[1],并且利用完全二叉树的性质,我们很容易求第i个结点的父结点(parent(i))、左孩子结点(left(i))、右孩子结点(right(i))的下标了,分别为:i/2、2i、2i+1;更重要的是,堆具有这样一个性质,对除根以外的每个结点i,A[parent(i)]≥A[i]。即除根结点以外,所有结点的值都不得超过其父结点的值,这样就推出,堆中的最大元素存放在根结点中,且每一结点的子树中的结点值都小于等于该结点的值,这种堆又称为“大根堆”;反之,对除根以外的每个结点i,A[parent(i)]≤A[i]的堆,称为“小根堆”。四、堆的操作用堆的关键部分是两个操作:put操作,即往堆中加入一个元素;get操作,即从堆中取出并删除一个元素。1、往堆中加入一个元素的算法(put)如下:(1)在堆尾加入一个元素,并把这个结点置为当前结点。(2)比较当前结点和它父结点的大小如果当前结点小于父结点,则交换它们的值,并把父结点置为当前结点。转(2)。如果当前结点大于等于父结点,则转(3)。(3)结束。重复n次put操作,即可建立一个小根堆。我们举一个例子看看具体过程:设n=10,10堆的数量分别为:3517642541。设一个堆结构heap[11],现在先考虑用put操作建一个小根堆,具体方法是每次读入一个数插入到堆尾,再通过调整使得满足堆的性质(从堆尾son=len开始,判断它与父结点son/2的大小,若heap[son]
=heap[son/2]为止)。开始时堆的长度len=0。实际上,我们也可以直接用完全二叉树的形式描述出这个过程,得到如下的一棵完全二叉树(堆):voidput(intd)//heap[1]为堆顶{intnow,next;heap[++heap_size]=d;now=heap_size;while(now>1){next=now>>1;if(heap[now]>=heap[next])break;swap(heap[now],heap[next]);now=next;}}使用C++标准模板库STL(需要头文件):voidput(intd){heap[++heap_size]=d;//push_heap(heap+1,heap+heap_size+1);//大根堆push_heap(heap+1,heap+heap_size+1,greater());//小根堆}2、从堆中取出并删除一个元素的算法(get)如下:(1)取出堆的根结点的值。(2)把堆的最后一个结点(len)放到根的位置上,把根覆盖掉。把堆的长度减一。(3)把根结点置为当前父结点pa。(4)如果pa无儿子(pa>len/2),则转(6);否则,把pa的两(或一)个儿子中值最小的那个置为当前的子结点son。(5)比较pa与son的值,如果fa的值小于或等于son,则转(6);否则,交换这两个结点的值,把pa指向son,转(4)。(6)结束。intget()//heap[1]为堆顶{intnow=1,next,res=heap[1];heap[1]=heap[heap_size--];while(now*2<=heap_size){next=now*2;if(next):intget(){//pop_heap(heap+1,heap+heap_size+1);//大根堆pop_heap(heap+1,heap+heap_size+1,greater());//小根堆returnheap[heap_size--];}五、堆的应用例1、合并果子(fruit)【问题描述】在一个果园里,多多已经将所有的果子打了下来,而且按果子的不同种类分成了不同的堆。多多决定把所有的果子合成一堆。每一次合并,多多可以把两堆果子合并到一起,消耗的体力等于两堆果子的重量之和。可以看出,所有的果子经过n-1次合并之后,就只剩下一堆了。多多在合并果子时总共消耗的体力等于每次合并所耗体力...