专题4：动态几何之存在性问题探讨VIP免费

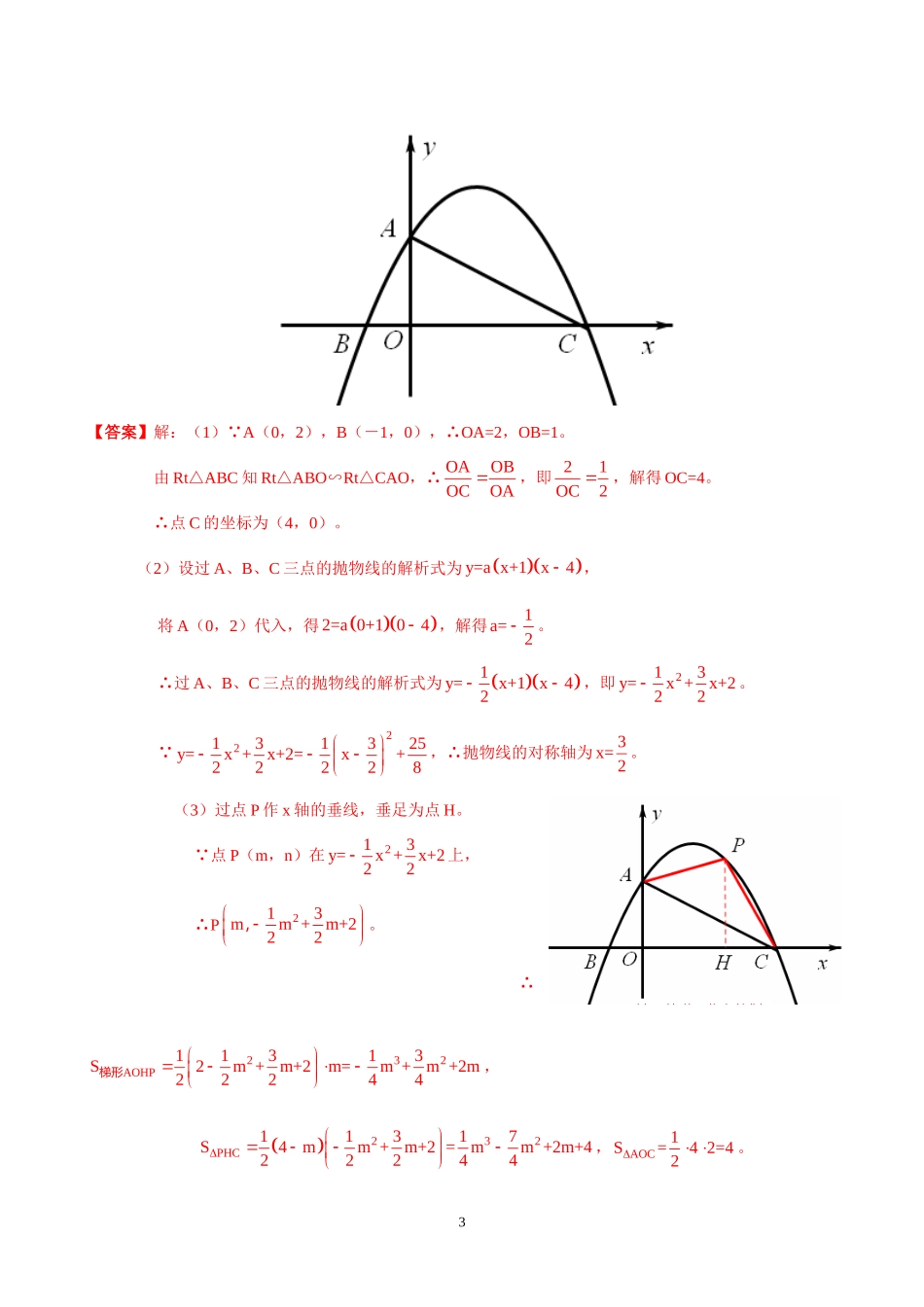
【2013年中考攻略】专题4：动态几何之存在性问题探讨动态题是近年来中考的的一个热点问题，动态包括点动、线动和面动三大类，解这类题目要“以静制动”，即把动态问题，变为静态问题来解，而静态问题又是动态问题的特殊情况。常见的题型包括最值问题、面积问题、和差问题、定值问题和存在性问题等。前面我们已经对最值问题、面积问题、和差问题、定值问题进行了探讨，本专题对存在性问题进行探讨。结合2012年全国各地中考的实例，我们从七方面进行动态几何之存在性问题的探讨：（1）等腰（边）三角形存在问题；（2）直角三角形存在问题；（3）平行四边形存在问题；（4）矩形、菱形、正方形存在问题；（5）梯形存在问题；（6）全等、相似三角形存在问题；（7）其它存在问题。一、等腰（边）三角形存在问题：典型例题：例1：（2012广西崇左10分）如图所示，抛物线cbxaxy2（a≠0）的顶点坐标为点A（－2，3），且抛物线cbxaxy2与y轴交于点B（0，2）.（1）求该抛物线的解析式；（2）是否在x轴上存在点P使△PAB为等腰三角形，若存在，请求出点P的坐标；若不存在，请说明理由；（3）若点P是x轴上任意一点，则当PA－PB最大时，求点P的坐标.【答案】解：（1） 抛物线的顶点坐标为A(－2，3)，∴可设抛物线的解析式为2ya(x2)3。由题意得2a(02)32，解得1a4。∴物线的解析式为21y(x2)34，即21yxx24。（2）设存在符合条件的点P，其坐标为（p，0），则PA2=22(2p)3，PB=22p2，AB2=22(32)251当PA=PB时，22(2p)3=22p2，解得9p4；当PA=PB时，22(2p)3=5，方程无实数解；当PB=AB时，22p2=5，解得p1。∴x轴上存在符合条件的点P，其坐标为（94，0）或（-1,0）或（1,0）。（3） PA－PB≤AB，∴当A、B、P三点共线时，可得PA－PB的最大值，这个最大值等于AB，此时点P是直线AB与x轴的交点。设直线AB的解析式为y=kx+b，则b22kb3，解得1k2b2。∴直线AB的解析式为1yx22，当1yx22=0时，解得x4。∴当PA－PB最大时，点P的坐标是（4，0）。【考点】二次函数综合题，待定系数法，曲线上点的坐标与方程的关系，等腰三角形的判定和性质。【分析】（1）由已知用待定系数法，设顶点式求解。（2）分PA=PB、PA=PB、PB=A三种情况讨论即可。（3）求得PA－PB最大时的位置，即可求解。例2：（2012辽宁朝阳14分）已知，如图，在平面直角坐标系中，Rt△ABC的斜边BC在x轴上，直角顶点A在y轴的正半轴上，A（0，2），B（－1，0）。（1）求点C的坐标；（2）求过A、B、C三点的抛物线的解析式和对称轴；（3）设点P（m，n）是抛物线在第一象限部分上的点，△PAC的面积为S，求S关于m的函数关系式，并求使S最大时点P的坐标；（4）在抛物线对称轴上，是否存在这样的点M，使得△MPC（P为上述（3）问中使S最大时点）为等腰三角形？若存在，请直接写出点M的坐标；若不存在，请说明理由。2【答案】解：（1） A（0，2），B（－1，0），∴OA=2，OB=1。由Rt△ABC知Rt△ABO∽Rt△CAO，∴OAOBOCOA，即21OC2，解得OC=4。∴点C的坐标为（4，0）。（2）设过A、B、C三点的抛物线的解析式为y=ax+1x4，将A（0，2）代入，得2=a0+104，解得1a=2。∴过A、B、C三点的抛物线的解析式为1y=x+1x42，即213y=x+x+222。 22131325y=x+x+2=x+22228，∴抛物线的对称轴为3x=2。（3）过点P作x轴的垂线，垂足为点H。 点P（m，n）在213y=x+x+222上，∴P213mm+m+222，。∴232AOHP11313S2m+m+2m=m+m+2m22244梯形，232PHC11317S4mm+m+2=mm+2m+422244，AOC1S=42=42。3∴32322PHCAOCAOHP1317S=S+SS=m+m+2m+mm+2m+44=m+4m4444梯形。 22S=m+4m=m2+4，∴当m2时，S最大。当m2时，213n=2+2+2=322。∴点P的坐标为（2，3）。（4）存在。点M的坐标为（31,22）或（33,322）或（33,322-）或（3,3102）或（3,1023-）。【考点】二次函数综合题，相似三角形的判定和性质，待定系数...