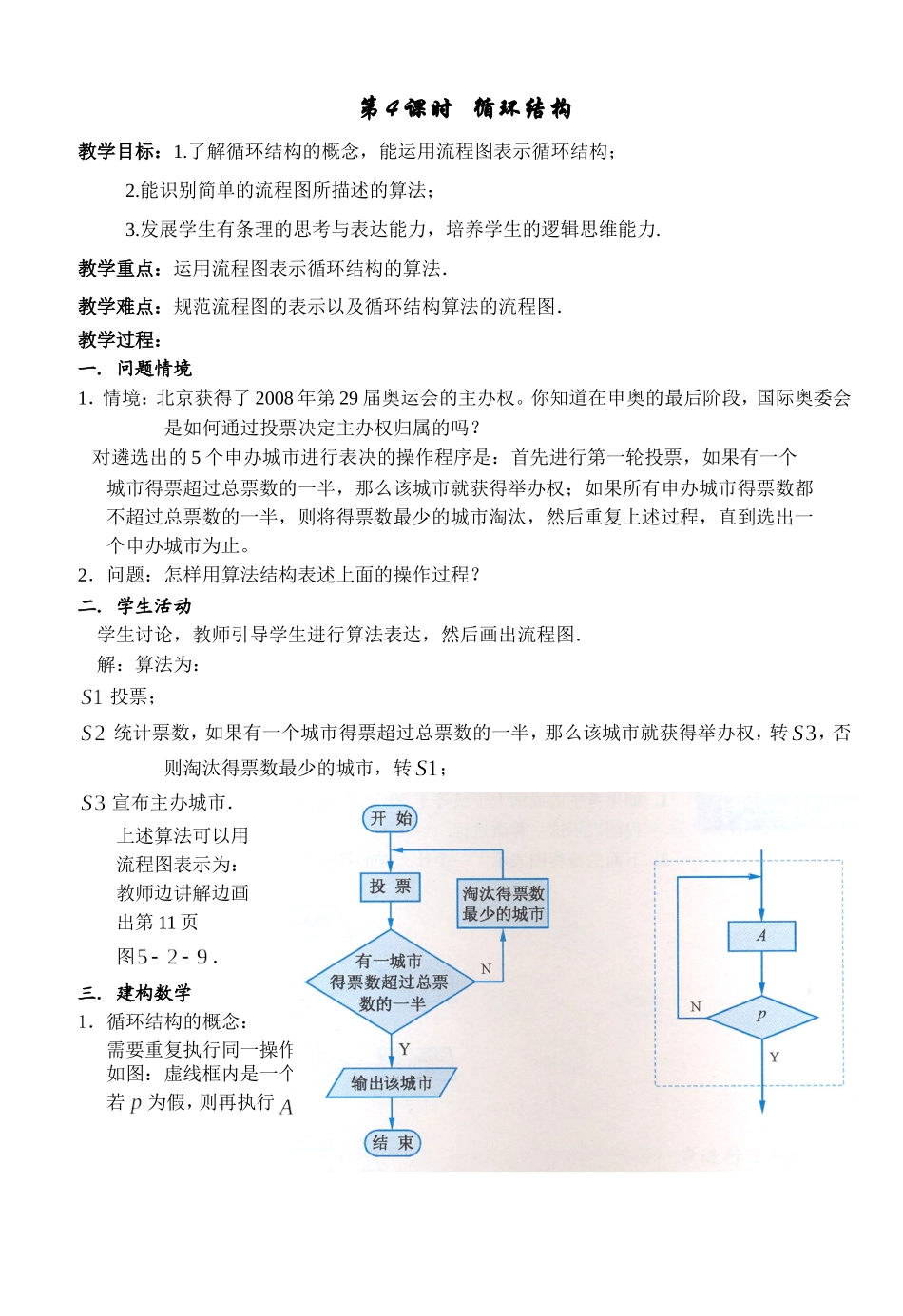
第4课时循环结构教学目标:1.了解循环结构的概念,能运用流程图表示循环结构;2.能识别简单的流程图所描述的算法;3.发展学生有条理的思考与表达能力,培养学生的逻辑思维能力.教学重点:运用流程图表示循环结构的算法.教学难点:规范流程图的表示以及循环结构算法的流程图.教学过程:一.问题情境1.情境:北京获得了2008年第29届奥运会的主办权。你知道在申奥的最后阶段,国际奥委会是如何通过投票决定主办权归属的吗?对遴选出的5个申办城市进行表决的操作程序是:首先进行第一轮投票,如果有一个城市得票超过总票数的一半,那么该城市就获得举办权;如果所有申办城市得票数都不超过总票数的一半,则将得票数最少的城市淘汰,然后重复上述过程,直到选出一个申办城市为止。2.问题:怎样用算法结构表述上面的操作过程?二.学生活动学生讨论,教师引导学生进行算法表达,然后画出流程图.解:算法为:投票;统计票数,如果有一个城市得票超过总票数的一半,那么该城市就获得举办权,转,否则淘汰得票数最少的城市,转;宣布主办城市.上述算法可以用流程图表示为:教师边讲解边画出第11页图.三.建构数学1.循环结构的概念:需要重复执行同一操作的结构称为循环结构.如图:虚线框内是一个循环结构,先执行框,再判断给定的条件是否为假;若为假,则再执行,再判断给定的条件是否为假……,如此反复,直到为真,该循1环过程结束。2.说明:(1)循环结构主要用在反复做某项工作的问题中;(2)循环结构是通过选择结构来实现。3.思考:教材第12页图所示的算法中,哪些步骤构成了循环结构?循环结构要素:循环变量和初始条件、循环体、循环的终止条件。四.数学运用1.循环结构举例例1.(教材第12页例4)写出求值的一个算法,并画出流程图.解:算法1:逐一相乘;算法2:;{使};{使};{求,乘积结果仍放在变量中};{使的值增加1}如果,转,否则输出。说明:1.算法2中各种符号的意义;2.算法2不仅形式简练,而且具有通用性、灵活性。其中,,组成一个循环,在实现算法时要反复多次执行,,步骤,直到执行时,经过判断,乘数已超过规定的数为止。算法流程图如右.【思考】将算法二作如下修改,注意与算法二的区别。算法三:S1设一个变量T=1S2设另一个变量为i=2S3如果i不大于5,T←T×i,执行S4,否则转到S5S4i←i+1,重复S3S5输出T分析:在算法三中,执行S3、S4是有条件的,当i小于等于5时才可以。流程图:2Y开始T←1I←2i←i+1I≤5N输出T结束T←T×i上述循环结构用示意图表示为:【总结】图A中,循环体一直执行,直到条件成立时退出循环,这种循环称为直到型循环。图B中,当条件成立时循环体才执行,这种循环称为当型循环。练习1:写出求值的一个算法,并画出流程图.例2.设计一个计算10个数平均数的算法,并画出流程图.分析:由于需要依次输入10个数,并计算它们的和,因此,需要用一个循环结构,并用一个变量存放数的累加和。在求出10个数的总和后,再除以10,就得到10个数的平均数。解:;{使};{使}输入;{输入一个数};{求,其和仍放在变量中};{使的值增加1}如果,转,{如果,退出循环};{将平均数存放到中}输出。{输出平均数}说明:1.本题中的第一步将赋值于,是为这些数的和建立存放空间;2.在循环结构中都有一个计数变量(本题中的)和累加变量(本题中的),计数变量用于记录循环次数(本题实质是为了记录输入的数的个数),累加变量用于输出结果。计数变量与累加变量一般是同步进行的,累加一次,计数一次。算法流程图如右.2.练习:课本第14页练习第1、2题.3NPY图BA练习1答案:;;;;如果,转,否则输出。练习2答案:将50个学生中成绩不低于80分的学生的学号和成绩打印出来。练习3:先写出计算的一个算法,再画出流程图.练习4:下面表示了一个什么样的算法?代表第个学生的学号,代表第个学生的成绩.()练习5:写出求值的一个算法,并画出流程图.[拓展提高]任意给定一个大于1的正整数n,设计一个算法对n是否为质数作出判断,并画出流程图。六.回顾小结1.循环结构的概念:2.用循环结构画流程图的三要素:3.直到型循环与当型循环的区别与联系:4.在...