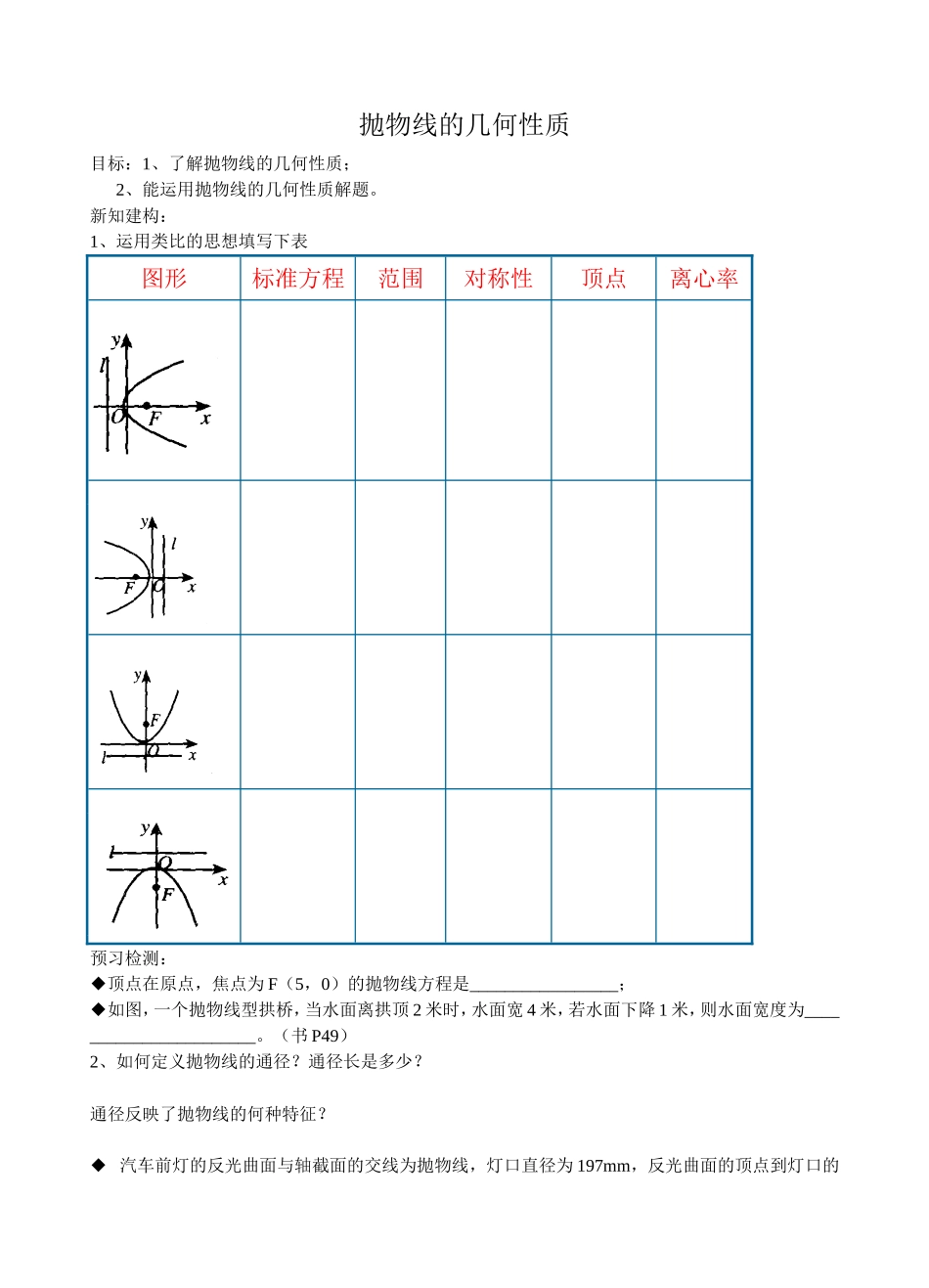
抛物线的几何性质目标:1、了解抛物线的几何性质;2、能运用抛物线的几何性质解题。新知建构:1、运用类比的思想填写下表图形标准方程范围对称性顶点离心率预习检测:◆顶点在原点,焦点为F(5,0)的抛物线方程是_________________;◆如图,一个抛物线型拱桥,当水面离拱顶2米时,水面宽4米,若水面下降1米,则水面宽度为_______________________。(书P49)2、如何定义抛物线的通径?通径长是多少?通径反映了抛物线的何种特征?◆汽车前灯的反光曲面与轴截面的交线为抛物线,灯口直径为197mm,反光曲面的顶点到灯口的距离是69mm。由抛物线的性质可知,当灯泡安装在抛物线的交点处时,经反光曲面反射后的光线是平行光线,为获得平行光线,应如何安装灯泡?例题分析例一:已知抛物线,焦点为F,准线为,过F的直线交抛物线与。⑴求、的值;⑵求AB(如果直线的倾斜角为,AB为多少)⑶判断以AB为直径的圆与准线的位置关系(3)求证:⑸过A作AN⊥,过B作BM⊥,垂足为N、M,设P为MN的中点,①求证:PF⊥AB,⊥NF。②设AB的中点为E,PE交抛物线与点Q,求证Q为PE中点;③求证:A、O、M三点共线.⑹设AB的中点为E,过E作EH⊥于H,EH交抛物线于G,求证FH⊥AB,且HG=EG=GF(6)若AB的垂直平分线交X轴于R,求证:FR=AB例二:已知抛物线的内接正三角形的一个顶点在原点,另两个顶点在抛物线上,求此正三角形的边长与面积。变2:已知抛物线的内接三角形的一个顶点在原点,另两个顶点A、B在抛物线上,若△AOB的重心恰好是抛物线的焦点,求A、B两点的坐标。变2:将变1中的垂心改为重心变3:已知与顶点在原点O,焦点在X轴上的抛物线C交于A、B两点且△AOB的垂心恰好是抛物线的焦点,求抛物线C的标准方程。例三、已知抛物线的方程为y²=4x,直线l过定点P(-2,1),斜率为k,当k为何值时,直线l与抛物线y²=4x,只有一个公共点;有两个公共点;没有公共点?变1:求过点(0,1)且与抛物线y²=4x只有一个公共点的直线方程。变2:过点(-1,2)且与抛物线y²=4x只有一个公共点的直线有条过点(1,2)且与抛物线y²=4x只有一个公共点的直线有条过点(2,1)且与抛物线y²=4x只有一个公共点的直线有条小结:例四、求抛物线被点P(-1,1)所平分的弦所在的直线方程变:过点(0,-2)的直线与抛物线交于A、B两点,若线段AB中点M的横坐标为2,求直线AB的方程例三:1、在抛物线上求一点P,使P到直线的距离最短,并求出距离的最小值。2、P为抛物线上一点,点A(a,0),求PA的最小值。3、已知抛物线和定点A(2,2),F为焦点,P为抛物线上一动点,则PA+PF的最小值为。变:定长为5的线段AB的两个端点在抛物线上移动,则线段AB的中点M到Y轴的最小距离为。例五:正方形的一条边AB在直线上,顶点C、D在抛物线上,求正方形的边长。例六:已知A、B是抛物线上两点,满足OA⊥OB(O为坐标原点)。求证:(1)A、B两点横坐标之积,纵坐标之积分别为定值;(2)直线AB必过一定点;(3)△AOB面积的最小值为4.例六:如图,在平面直角坐标系xOy中,过y轴正上方一点C(0,c)任作一直线,与抛物线y=x2相交于A、B两点,一条垂直于x轴的直线,分别与线段AB和直线交于点P、Q.(1)若=2,求c的值;巩固练习1、已知抛物线上一点到焦点的距离为5,则这点的坐标为_____________;2、已知抛物线的顶点是双曲线的中心,而焦点是双曲线的左顶点,则抛物线的方程是__________________________;3、以抛物线焦半径为直径的园与轴的位置关系是_________________;4、抛物线的通径为_____________________;5、已知直线与抛物线交与A、B两点,且经过抛物线的焦点F,A点坐标为(8,8),则线段AB的中点到准线的距离为_________________;6、过抛物线的焦点的直线倾斜角为600,则弦长为__________________;7、过抛物线焦点的直线交抛物线于A、B两点,已知|AB|=10,O为坐标原点,则ΔABC重心的横坐标为_______8、已知抛物线上有点,且,若线段AB、BC在轴上的射影之长相等,求证:A、B、C三点到焦点的距离顺次成等差数列。9、过抛物线焦点F的直线交抛物线于A,B两点,通过点A和抛物线顶点的直线交抛物线的准线于点D,求证:直线DB平行于抛物线的对称轴。