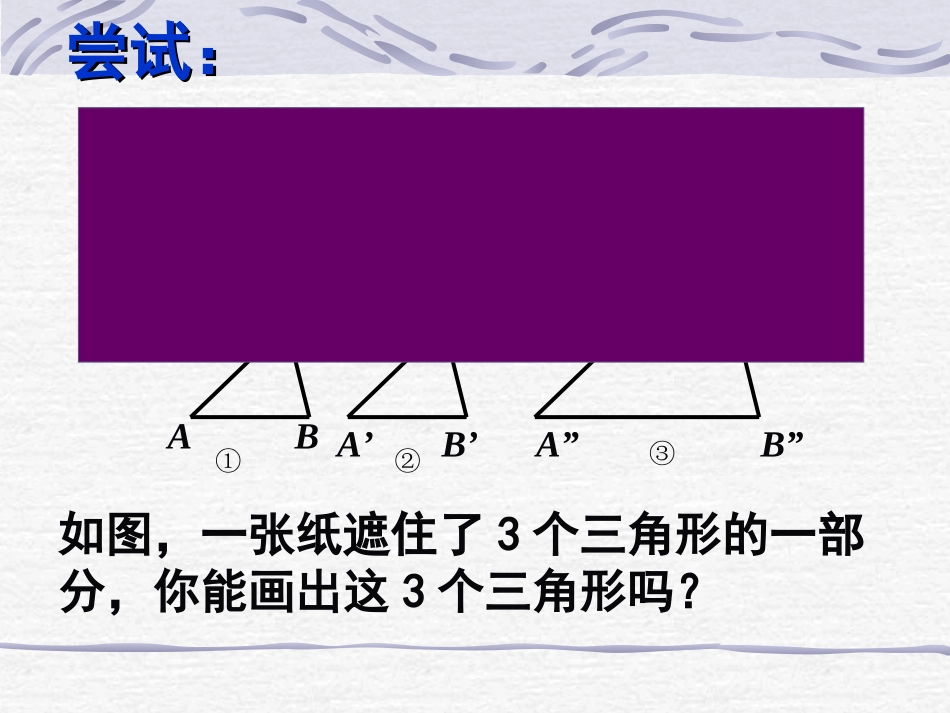
初中数学八年级下册(苏科版)10.4探索三角形相似的条件(1)10.4探索三角形相似的条件(1)无锡市清名桥中学王旭奕如何判断两个三角形相似?思考:是否还有其它的判定方法呢?ABCA’B’C’∵∠A=∠A’,∠B=∠B’,∠C=∠C’,ABACBC==A'B'A'C'B'C'∴△ABC∽A'B'C'△如图,一张纸遮住了3个三角形的一部分,你能画出这3个三角形吗?尝试:尝试:BAA’A”B’B”①②③如果∠A=∠A′,B∠=∠B′,AB=A′B′,那么图(1)与图(2)的两个三角形全等吗?思考:A”ABA’B’B”①②③CC’C”如果∠A=∠A”,∠B=∠B”,2AB=A”B”,那么图(1)与图(3)的两个三角形相似吗?如果把2AB=A”B”改为kAB=A”B”,这两个三角形还相似吗?尝试:尝试:A”ABA’B’B”①②③CC’C”交流讨论判定方法1:如果一个三角形的两个角与另一个三角形的两个角对应相等,那么这两个三角形相似。简写:两角对应相等,两三角形相似.∴△ABC∽△A'B'C'∵∠A=∠A’,∠B=∠B’()两角对应相等,两三角形相似例题欣赏例1、如图,在△ABC和△A′B′C′中,已知∠A=50°,∠B=∠B′=60°,∠C′=70°,△ABC与△A′B′C′相似吗?为什么?如图,已知点D,E分别在AB,AC或它们的延长线上,且∠1=∠2,分别指出图中的相似三角形。△ADE∽△ACB△ADE∽△ABC△ADC∽△ACB△ADE∽△ACB看谁反应快:注意隐含条件:公共角相等、对顶角相等。练习1:11122221DEAABDECCBCCBDDBEAACBDA如图,Rt△ABC中,CD是斜边AB上的高,(1)试说明:△ABC∽△ACDABAC=ACAD(2)根据△ABC∽△ACD有∴AC2=AD·AB,类似地,你还可以得到哪些结论?BC2=AD·AB,AC2=AD·AB,练习2:△ABC∽△CBD∽△ACD图中还有相似三角形吗?如图,DE∥BC,分别交AB、AC于点D、E,△ADE与△ABC相似吗?为什么?【变题】如图,点A、B、D与点A、C、E分别在一条直线上,如果DE∥BC,△ADE与△ABC相似吗?为什么?ADEBCEDABCABCED思考:∵DE∥BC∴△ADE∽△ABCADEBCEDABCABCED※这是两个最常见的相似三角形基本模型:“A”型和“X”型见平行,想相似平行于三角形一边的直线与其他两边(或两边的延长线)相交,所构成的三角形与原三角形相似.判定方法2:如图,AB∥CD,AD∥BC,过A的直线交BD、BC和DC的延长线于E、F、G。(1)与△ABD相似的三角形有_________.(2)与△AED相似的三角形有_________.(3)与△AEB相似的三角形有_________.(4)与△GFC相似的三角形有__________.练习3:ABCDEFG△CDB△FEB△GED△GAD、△AFB练习4:实际应用如图,在测量小玻璃管管径的量具上,AB长为5mm,AC长为50mm.如果玻璃管的管径DE正好对着量具上30mm处(DE∥AB).那么管径DE的长等于多少?55030发散探究过△ABC的边AB上一点D作一条直线与另一边AC相交,截得的小三角形与△ABC相似,这样的直线有几条?请把它们一一作出来。这样的直线有几条?CD●AB练习5:小结:本节课你有哪些收获?判定方法1:两角对应相等,两三角形相似.判定方法2:“见平行,想相似”在直角三角形ABC的直角边AC上有一点定P(点P与点A,C不重合),过点P作直线截ΔABC,使截得的三角形与ΔABC相似,满足条件的直线共有_________条.尝试、探究: