弧弦圆心角的关系VIP免费

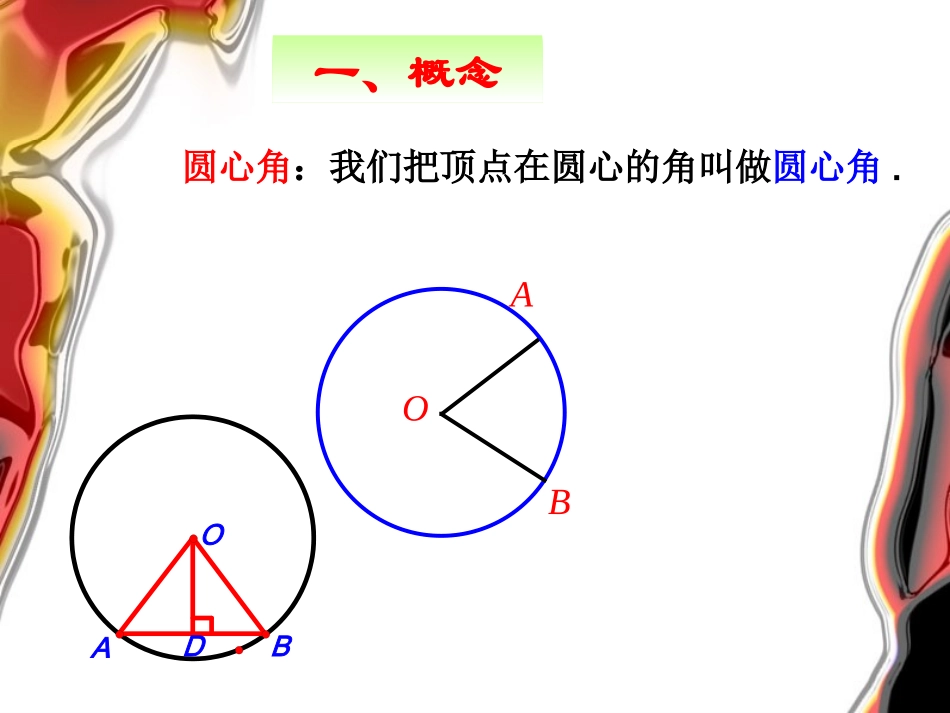
·圆心角：我们把顶点在圆心的角叫做圆心角.OBA一、概念DABO根据旋转的性质，将圆心角∠AOB绕圆心O旋转到∠A′OB′的位置时，∠AOB＝∠A′OB′，射线OA与OA′重合，OB与OB′重合．而同圆的半径相等，OA=OA′，OB=OB′，∴点A与A′重合，B与B′重合．·OAB探究·OABA′B′A′B′二、'',ABAB''.ABAB∴重合，AB与A′B′重合．''ABAB与如图，将圆心角∠AOB绕圆心O旋转到∠A’OB’的位置，你能发现哪些等量关系？为什么？在同圆或等圆中，相等的弧所对的圆心角_____，所对的弦________；在同圆或等圆中，相等的弦所对的圆心角______，所对的弧_________．弧、弦与圆心角的关系定理在同圆或等圆中，相等的圆心角所对的弧相等，所对的弦也相等．相等相等相等相等同圆或等圆中，两个圆心角、两条弧、两条弦中有一组量相等，它们所对应的其余各组量也相等．同圆或等圆中，两个圆心角、两条弧、两条弦中有一组量相等，它们所对应的其余各组量也相等．三、定理如图，AB、CD是⊙O的两条弦．（1）如果AB=CD，那么___________，_________________．（2）如果，那么____________，_____________．（3）如果∠AOB=COD∠，那么_____________，_________．（4）如果AB=CD，OE⊥AB于E，OF⊥CD于F，OE与OF相等吗？为什么？·CABDEFOABCDAOBCODAB=CDABCDAOBCOD,,11,22ABCDAECFOAOCR.OEOFOEABOFCDAEABCFCDtAOERtCOFOEOF证明：又＝＝又＝AB=CD四、练习ABCD证明：∴AB=AC．又∠ACB=60°，∴AB=BC=CA.∴∠AOB＝∠BOC＝∠AOC.·ABCOABAC，五、例题例1如图,在⊙O中，，∠ACB=60°，求证∠AOB=∠BOC=∠AOC.ABAC＝如图，AB是⊙O的直径，∠COD=35°，求∠AOE的度数．·AOBCDEBCCDDEBOC=COD=DOE=35180335AOE75解：,BCCDDE＝六、练习七、思考OADBC如图，已知AB、CD为的两条弦，，求证AB＝CD.DCABO