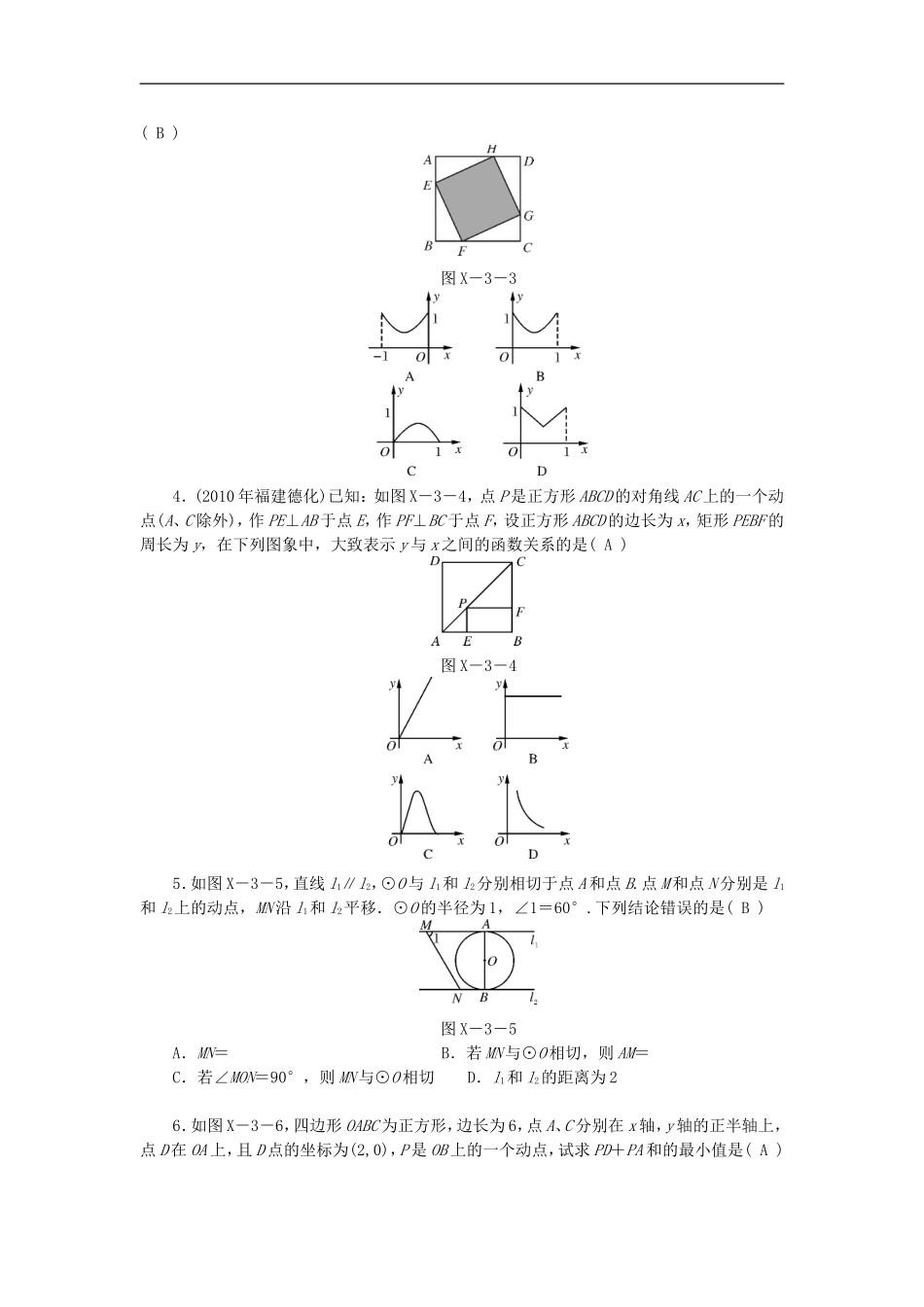
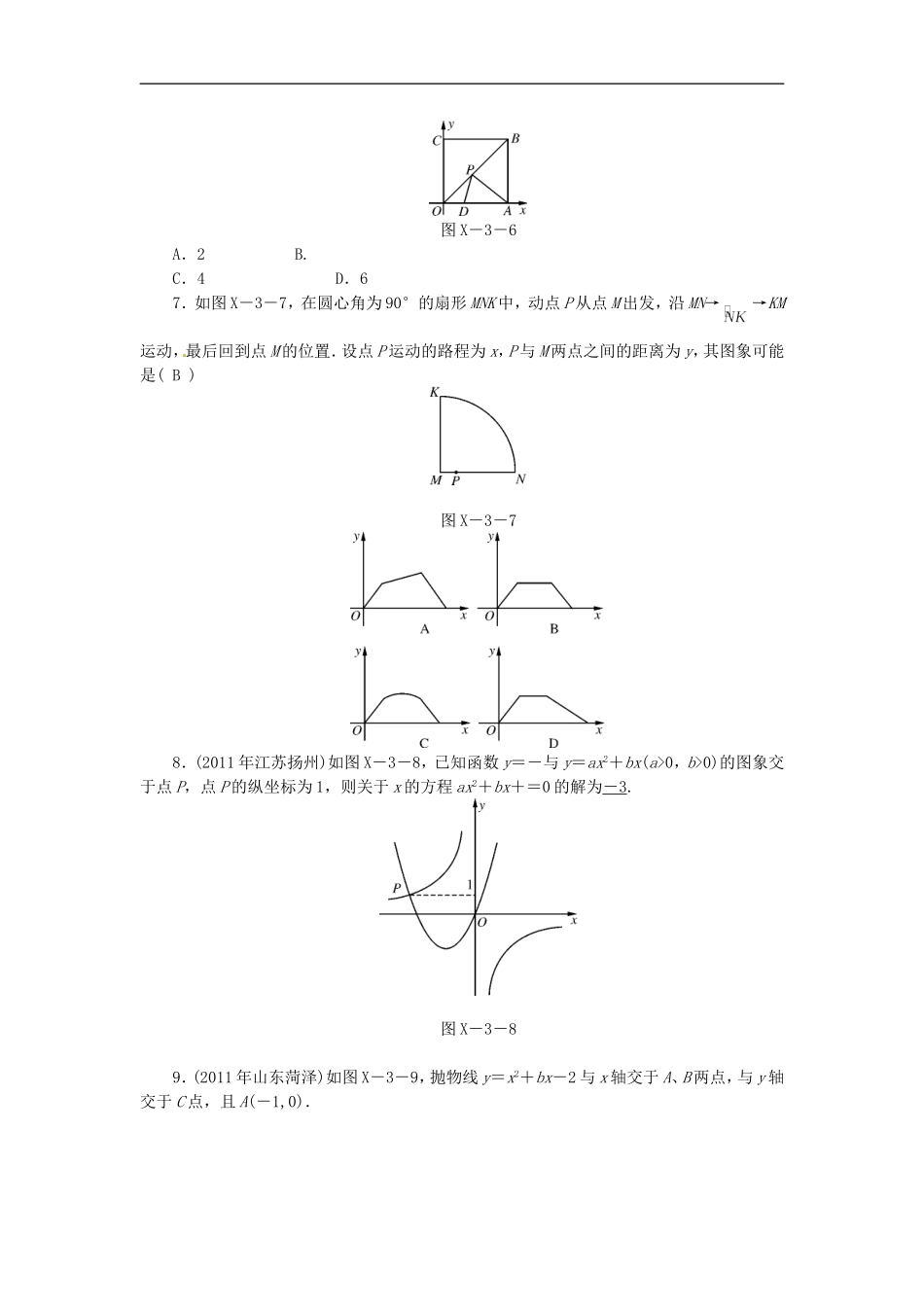
中考专题突破三数形结合思想专题训练1.(2011年安徽)如图X-3-1,P是菱形ABCD的对角线AC上一动点,过P垂直于AC的直线交菱形ABCD的边于M、N两点,设AC=2,BD=1,AP=x,△AMN的面积为y,则y关于x的函数图象的大致形状是(C)图X-3-12.(2011年山东威海)如图X-3-2,在正方形ABCD中,AB=3cm,动点M自A点出发沿AB方向以每秒1cm的速度运动,同时动点N自A点出发沿折线AD—DC—CB以每秒3cm的速度运动,到达B点时运动同时停止,设△AMN的面积为y(cm2),运动时间为x(秒),则下列图象中能大致反映y与x之间的函数关系的是(B)图X-3-23.(2011年甘肃兰州)如图X-3-3,正方形ABCD的边长为1,E、F、G、H分别为各边上的点,且AE=BF=CG=DH,设小正方形EFGH的面积为S,AE为x,则S关于x的函数图象大致是(B)图X-3-34.(2010年福建德化)已知:如图X-3-4,点P是正方形ABCD的对角线AC上的一个动点(A、C除外),作PE⊥AB于点E,作PF⊥BC于点F,设正方形ABCD的边长为x,矩形PEBF的周长为y,在下列图象中,大致表示y与x之间的函数关系的是(A)图X-3-45.如图X-3-5,直线l1∥l2,⊙O与l1和l2分别相切于点A和点B.点M和点N分别是l1和l2上的动点,MN沿l1和l2平移.⊙O的半径为1,∠1=60°.下列结论错误的是(B)图X-3-5A.MN=B.若MN与⊙O相切,则AM=C.若∠MON=90°,则MN与⊙O相切D.l1和l2的距离为26.如图X-3-6,四边形OABC为正方形,边长为6,点A、C分别在x轴,y轴的正半轴上,点D在OA上,且D点的坐标为(2,0),P是OB上的一个动点,试求PD+PA和的最小值是(A)图X-3-6A.2B.C.4D.67.如图X-3-7,在圆心角为90°的扇形MNK中,动点P从点M出发,沿MN→→KM运动,最后回到点M的位置.设点P运动的路程为x,P与M两点之间的距离为y,其图象可能是(B)图X-3-78.(2011年江苏扬州)如图X-3-8,已知函数y=-与y=ax2+bx(a>0,b>0)的图象交于点P,点P的纵坐标为1,则关于x的方程ax2+bx+=0的解为-3.图X-3-89.(2011年山东菏泽)如图X-3-9,抛物线y=x2+bx-2与x轴交于A、B两点,与y轴交于C点,且A(-1,0).图X-3-9(1)求抛物线的解析式及顶点D的坐标;(2)判断△ABC的形状,证明你的结论;(3)点M(m,0)是x轴上的一个动点,当MC+MD的值最小时,求m的值.解:(1)把点A(-1,0)的坐标代入抛物线的解析式y=x2+bx-2,整理后解得b=-,所以抛物线的解析式为y=x2-x-2.顶点D.(2) AB=5,AC2=OA2+OC2=5,BC2=OC2+OB2=20,∴AC2+BC2=AB2.∴△ABC是直角三角形.(3)作出点C关于x轴的对称点C′,则C′(0,2),OC′=2.连接C′D交x轴于点M,根据轴对称性及两点之间线段最短可知,MC+MD的值最小.设抛物线的对称轴交x轴于点E.△C′OM∽△DEM.∴=.∴=.∴m=.10.(2011年湖南邵阳)如图X-3-10,在平面直角坐标系Oxy中,已知点A,点C(0,3),点B是x轴上的点(位于点A右侧),以AB为直径的圆恰好经过点C.图X-3-10(1)求∠ACB的度数;(2)已知抛物线y=ax2+bx+3经过A、B两点,求抛物线的解析式;(3)线段BC上是否存在点D,使△BOD为等腰三角形?若存在,则求出所有符合条件的点D的坐标;若不存在,请说明理由.解:如图D57,(1)90°图D57(2) △AOC∽△COB,∴=,又 A(-,0),点C(0,3),∴AO=,OC=3,∴所以解得:OB=4,∴B(4,0),把A、B两点坐标代入解得:y=-x2+x+3.(3)存在.直线BC的方程为3x+4y=12,设点D(x,y).①若BD=OD,则点D在OB的中垂线上,点D横坐标为2,纵坐标为,即D1(2,)为所求.②若OB=BD=4,则=,=,得y=,x=,点D2(,)为所求.11.(2011年广东汕头)如图X-3-11,抛物线y=-x2+x+1与y轴交于点A,过点A的直线与抛物线交于另一点B,过点B作BC⊥x轴,垂足为点C(3,0).图X-3-11(1)求直线AB的函数关系式;(2)动点P在线段OC上,从原点O出发以每秒一个单位的速度向C移动,过点P作垂直于x轴,交直线AB于点M,交抛物线于点N.设点P移动的时间为t秒,MN的长为s个单位,求s与t的函数关系式,并写出t的取值范围;(3)设(2)的条件下(不考虑点P与点O,点C重合的情况),连接CM、BN,当t为何值时,四边形BCMN为平行四边形?问对于所求的t的值,平行四边形BCM...