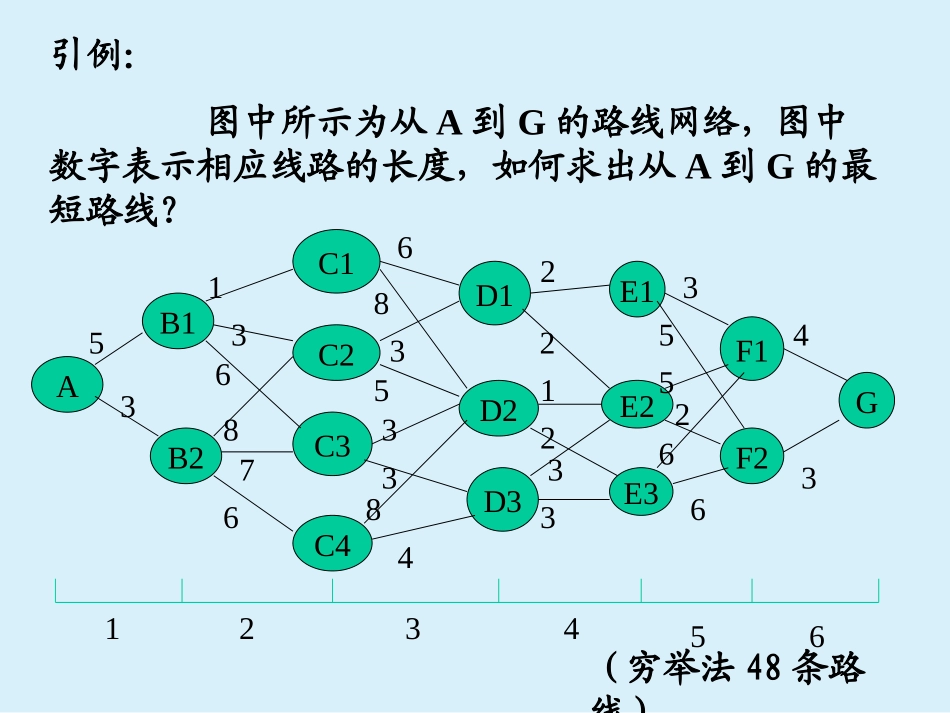
第四章动态规划(DynamicProgramming)重点:理解动态规划基本概念、最优化原理和基本方程;通过资源分配、生产与存储和设备更新等问题,学习应用动态规划解决多阶段决策问题;重点掌握动态规划模型结构、逆序算法原理、资源分配问题、生产与存储问题。难点为动态规划中状态变量、基本方程等的确定。•动态规划是用来解决多阶段决策过程最优化的一种数量方法。其特点在于,它可以把一个多阶段决策问题变换为几个相互联系的单阶段最优化问题,从而一个一个地去解决。•需指出:动态规划是求解某类问题的一种方法,是考察问题的一种途径,而不是一种算法。必须对具体问题进行具体分析,运用动态规划的原理和方法,划分阶段,建立相应的模型,然后再去求解。AB1B2C1C2C3C4D1D2D3E1E2E3F1F2G531368766835338422123335526643123456引例:图中所示为从A到G的路线网络,图中数字表示相应线路的长度,如何求出从A到G的最短路线?(穷举法48条路线)AB1B2C1C2C3C4D1D2D3E1E2E3F1F2G53136876683533842212333552663123456375976813109121316184AB1B2C1C2C3C4D1D2D3E1E2E3F1F2G5313687668353384221233355266312345615131315111313681095318174AB1B2C1C2C3C4D1D2D3E1E2E3F1F2G453136876683533822123335526643123456最短路的特性:如果已有从起点到终点的一条最短路,那么从最短路线上中间任何一点出发到终点的路线仍然是最短路。(证明用反证法)§1动态规划的研究对象和引例动态系统:包含随时间变化的因素和变量的系统。动态决策问题:系统所处的状态和时刻是进行决策的重要因素。找到不同时刻的最优决策以及整个过程的最优策略。12n状态决策状态决策状态状态决策全过程的最优阶段1、生产决策问题企业在生产过程中,由于需求是随时间变化的,因此企业为了获得全年的最佳生产效益,就要在整个生产过程中逐月或逐季度地根据库存和需求决定生产计划。多阶段决策问题的典型例子2、机器负荷分配问题某种机器高负荷低负荷g=g(u1)产品的年产量投入生产的机器数量机器的年完好率为a,0