2014年高考文科数学试题分类汇编VIP免费

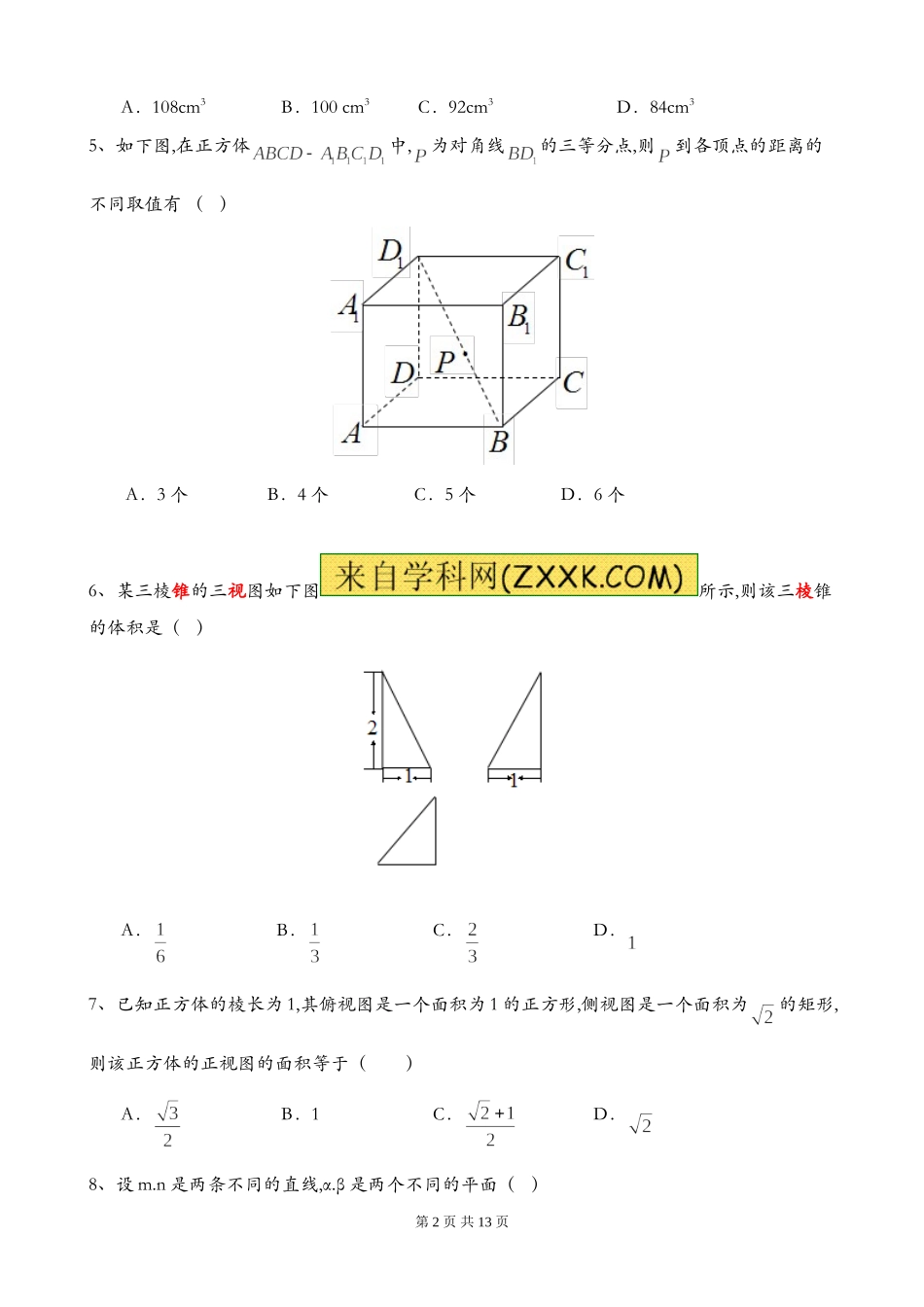
第1页共13页2014年高考文科数学试题分类汇编：立体几何详细解答一、选择题：1、某几何体的三视图如图所示,则该几何的体积为（）A．B．C．D．2、。已知正四棱锥中，,则与平面所成角的正弦值等于A．B．C．D．3、一个几何体的三视图如图所示,则该几何体可以是（）A．棱柱B．棱台C．圆柱D．圆台4、已知某几何体的三视图(单位:cm)如图所示,则该几何体的体积是（）第2页共13页A．108cm3B．100cm3C．92cm3D．84cm35、如下图,在正方体中,为对角线的三等分点,则到各顶点的距离的不同取值有（）A．3个B．4个C．5个D．6个6、某三棱锥的三视图如下图所示,则该三棱锥的体积是（）A．B．C．D．7、已知正方体的棱长为1,其俯视图是一个面积为1的正方形,侧视图是一个面积为的矩形,则该正方体的正视图的面积等于（）A．B．1C．D．8、设m.n是两条不同的直线,α.β是两个不同的平面（）第3页共13页A．若m∥α,n∥α,则m∥nB．若m∥α,m∥β,则α∥βC．若m∥n,m⊥α,则n⊥αD．若m∥α,α⊥β,则m⊥β9、已知三棱柱的6个顶点都在球的球面上,若,,,则球的半径为（）A．B．C．D．10、设为直线,是两个不同的平面,下列命题中正确的是（）A．若,,则B．若,,则C．若,,则D．若,,则11、一个四棱锥的侧棱长都相等,底面是正方形,其正(主)视图如下图所示该四棱锥侧面积和体积分别是（）A．45,8B．845,3C．84(51),3D．8,811、一几何体的三视图如右所示,则该几何体的体积为（）第4页共13页A．200+9πB．200+18πC．140+9πD．140+18π二、填空题：12、已知正四棱锥O-ABCD的体积为Error:Referencesourcenotfound,底面边长为Error:Referencesourcenotfound,则以O为球心,OA为半径的球的表面积为________.13、已知是球的直径上一点,,平面,为垂足,截球所得截面的面积为,则球的表面积为_______.14、某四棱锥的三视图如图所示,该四棱锥的体积为__________.15、某几何体的三视图如图所示,则其表面积为________16、已知圆和圆是球的大圆和小圆,其公共弦长等于球的半径,且圆与圆所在的平面所成角为60°，则球的表面积等于______.17、已知圆柱的母线长为,底面半径为,是上地面圆心,、是下底面圆周上两个不同的点,是母线,如图.若直线与所成角的大小为,则________.18、已知一个正方体的所有顶点在一个球面上.若球的体积为,则正方体的棱长为______.19、某几何体的三视图如图所示,则该几何体的体积是____________.第5页共13页20、如图,正方体的底面与正四面体的底面在同一平面α上,且AB//CD,则直线EF与正方体的六个面所在的平面相交的平面个数为_____________.21、如图,正方体的棱长为1,为的中点,为线段上的动点,过点的平面截该正方体所得的截面记为,则下列命题正确的是__________(写出所有正确命题的编号).①当时,为四边形;②当时,为等腰梯形;③当时,与的交第6页共13页点满足;④当时,为六边形;⑤当时,的面积为.三、解答题：22、如图,是圆的直径，垂直圆所在的平面，是圆上的点，(1)求证:平面;(2)设为的中点,为的重心，求证：//平面.23、如图,在在四棱锥中,⊥面,==2,==,=,∠=120°,为线段上的点.(1)证明:⊥面;(2)若是的中点,求与所成的角的正切值;(3)若满足⊥面,求的值.第7页共13页24、如图,四棱柱ABCD-A1B1C1D1的底面ABCD是正方形,O为底面中心,A1O⊥平面ABCD,12ABAA.(1)证明:A1BD//平面CD1B1;(2)求三棱柱ABD-A1B1D1的体积.25、如图,在四棱锥中,,,,,,,.(1)当正视图方向与向量的方向相同时,画出四棱锥的正视图.(要求标出尺寸,并画出演算过程);(2)若为的中点,求证://面;(3)求三棱锥的体积.第8页共13页25、如图1,在边长为1的等边三角形中,分别是边上的点,,是的中点,与交于点,将沿折起,得到如图2所示的三棱锥,其中.(1)证明://平面;(2)证明:平面;(3)当时,求三棱锥的体积.26、如图所示.在直菱柱ABC-A1B1C1中,∠BAC=90°,AB=AC=Error:Referencesourcenotfound,AA1=3,D是BC的中点,点E在菱BB1上运动.第9页共13页(1)证明:AD⊥C1E;(2)当异面直线AC,C1E所成的角为60°时,求三菱子C1-A2B1E的体积.27、如图,在四棱锥中,,,,平面底面,，和分别是和的中点,求证:(1)底面;(2)平面;(3)平面平面如图,三棱柱中,,,.第10页共13页(1)证明:;(2)若,,求三棱柱...