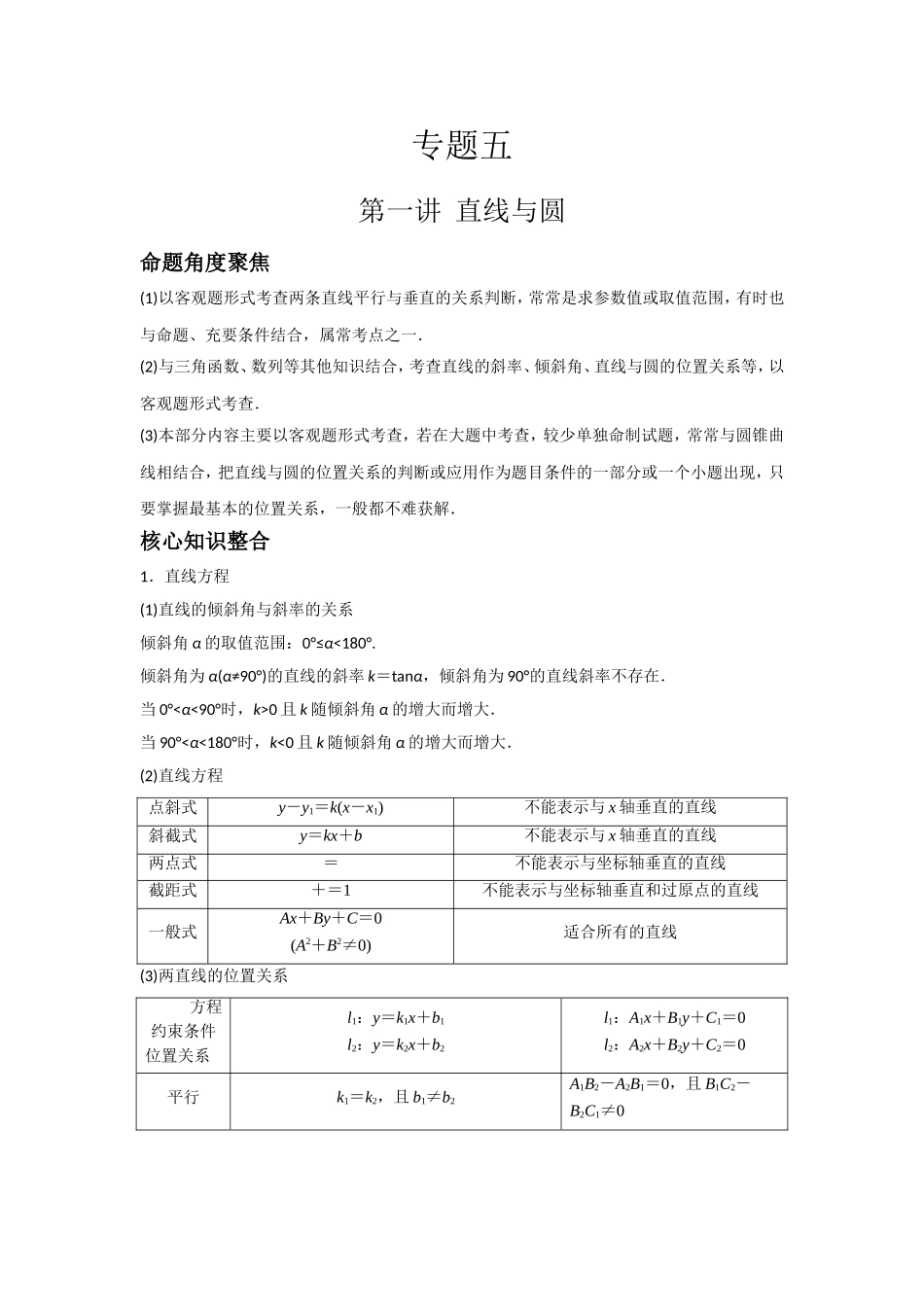
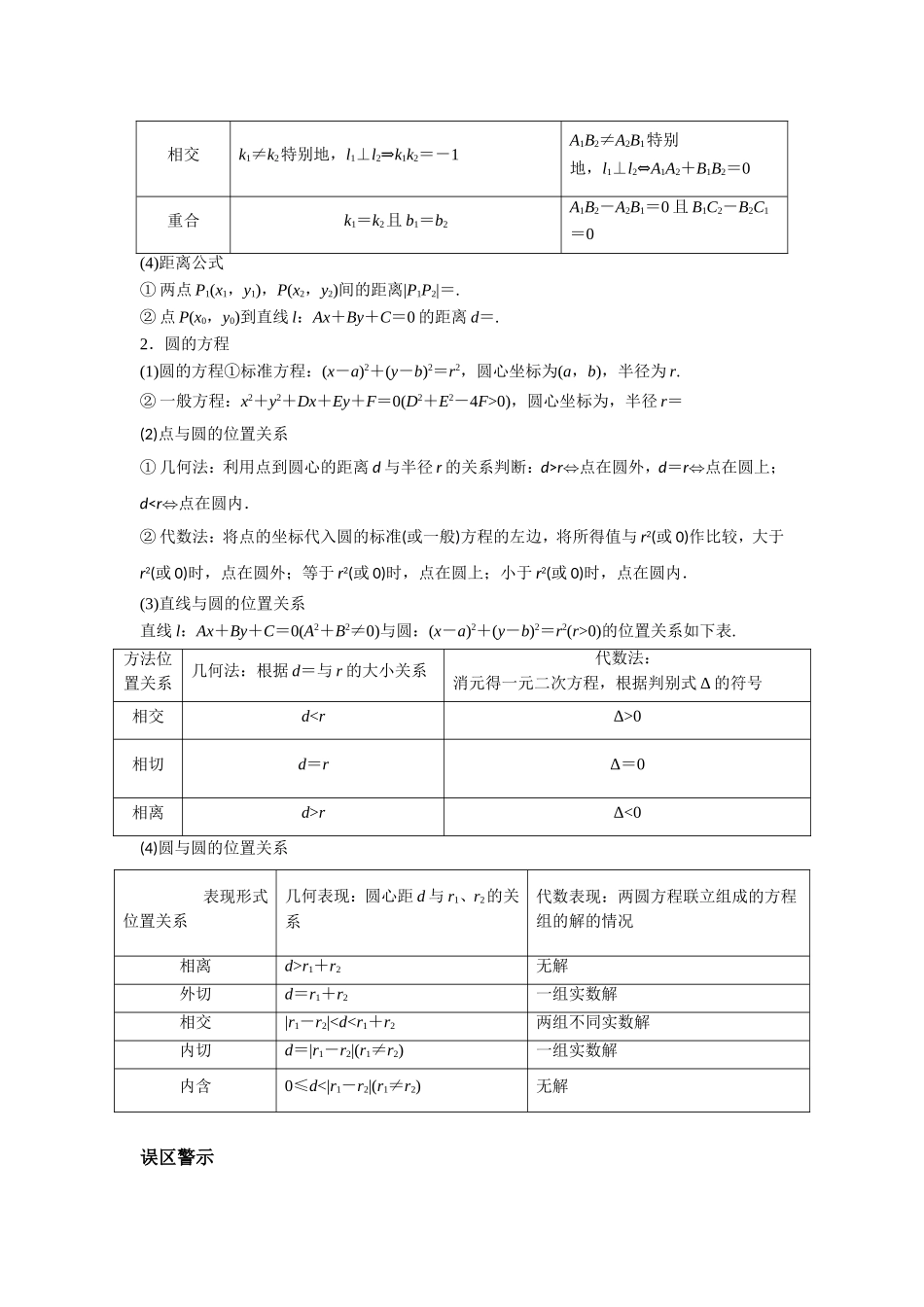
专题五第一讲直线与圆命题角度聚焦(1)以客观题形式考查两条直线平行与垂直的关系判断,常常是求参数值或取值范围,有时也与命题、充要条件结合,属常考点之一.(2)与三角函数、数列等其他知识结合,考查直线的斜率、倾斜角、直线与圆的位置关系等,以客观题形式考查.(3)本部分内容主要以客观题形式考查,若在大题中考查,较少单独命制试题,常常与圆锥曲线相结合,把直线与圆的位置关系的判断或应用作为题目条件的一部分或一个小题出现,只要掌握最基本的位置关系,一般都不难获解.核心知识整合1.直线方程(1)直线的倾斜角与斜率的关系倾斜角α的取值范围:0°≤α<180°.倾斜角为α(α≠90°)的直线的斜率k=tanα,倾斜角为90°的直线斜率不存在.当0°<α<90°时,k>0且k随倾斜角α的增大而增大.当90°<α<180°时,k<0且k随倾斜角α的增大而增大.(2)直线方程点斜式y-y1=k(x-x1)不能表示与x轴垂直的直线斜截式y=kx+b不能表示与x轴垂直的直线两点式=不能表示与坐标轴垂直的直线截距式+=1不能表示与坐标轴垂直和过原点的直线一般式Ax+By+C=0(A2+B2≠0)适合所有的直线(3)两直线的位置关系方程约束条件位置关系l1:y=k1x+b1l2:y=k2x+b2l1:A1x+B1y+C1=0l2:A2x+B2y+C2=0平行k1=k2,且b1≠b2A1B2-A2B1=0,且B1C2-B2C1≠0相交k1≠k2特别地,l1⊥l2⇒k1k2=-1A1B2≠A2B1特别地,l1⊥l2⇔A1A2+B1B2=0重合k1=k2且b1=b2A1B2-A2B1=0且B1C2-B2C1=0(4)距离公式①两点P1(x1,y1),P(x2,y2)间的距离|P1P2|=.②点P(x0,y0)到直线l:Ax+By+C=0的距离d=.2.圆的方程(1)圆的方程①标准方程:(x-a)2+(y-b)2=r2,圆心坐标为(a,b),半径为r.②一般方程:x2+y2+Dx+Ey+F=0(D2+E2-4F>0),圆心坐标为,半径r=(2)点与圆的位置关系①几何法:利用点到圆心的距离d与半径r的关系判断:d>r⇔点在圆外,d=r⇔点在圆上;d0)的位置关系如下表.方法位置关系几何法:根据d=与r的大小关系代数法:消元得一元二次方程,根据判别式Δ的符号相交d0相切d=rΔ=0相离d>rΔ<0(4)圆与圆的位置关系表现形式位置关系几何表现:圆心距d与r1、r2的关系代数表现:两圆方程联立组成的方程组的解的情况相离d>r1+r2无解外切d=r1+r2一组实数解相交|r1-r2|