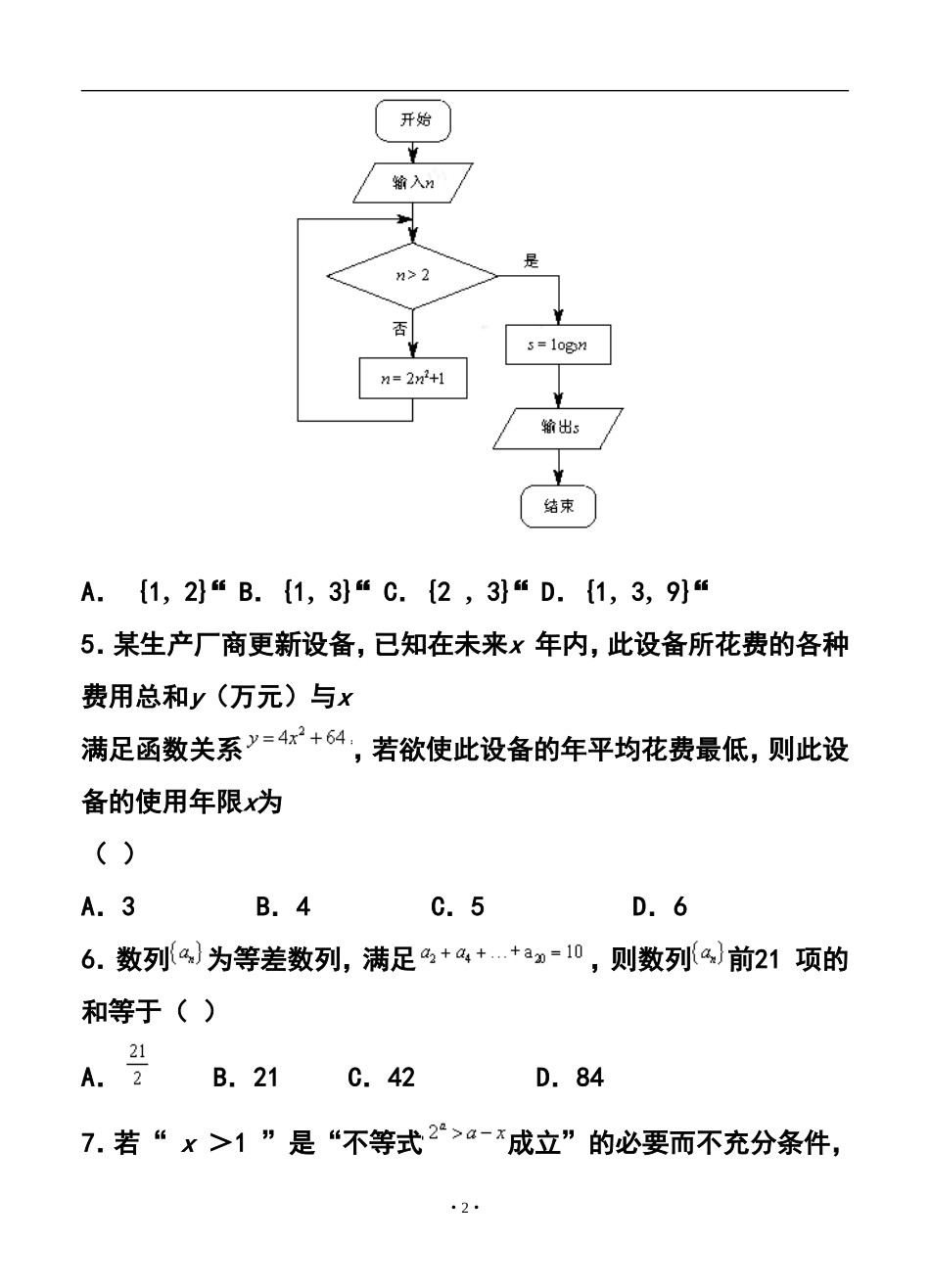
北京市西城区2015年高三二模试卷数学(理科)2015.5本试卷分第Ⅰ卷和第Ⅱ卷两部分,第Ⅰ卷1至2页,第Ⅱ卷3至6页,共150分.考试时长120分钟.考生务必将答案答在答题纸上,在试卷上作答无效。考试结束后,将本试卷和答题纸一并交回.1.设集合,集合,则AB=()A.(-1‚3)B.(1‚3]C.[1‚3)D.(-1‚3]2.已知平面向量,则实数k=()A.4B.-4C.8D.-83.设命题p:函数在R上为增函数;命题q:函数为奇函数.则下列命题中真命题是()4.执行如图所示的程序框图,若输入的,则输出的s属于()·1·A.{1‚2}B.{1‚3}C.{2‚3}D.{1‚3‚9}5.某生产厂商更新设备,已知在未来x年内,此设备所花费的各种费用总和y(万元)与x满足函数关系,若欲使此设备的年平均花费最低,则此设备的使用年限x为()A.3B.4C.5D.66.数列为等差数列,满足,则数列前21项的和等于()A.B.21C.42D.847.若“x>1”是“不等式成立”的必要而不充分条件,·2·则实数a的取值范围是()A.a>3B.a<3C.a>4D.a<48.在长方体,点M为AB1的中点,点P为对角线AC1上的动点,点Q为底面ABCD上的动点(点P,Q可以重合),则MP+PQ的最小值为()第Ⅱ卷(非选择题共110分)二、填空题:本小题共6小题,每小题5分,共30分.9.复数=____10.双曲线C:的离心率为;渐近线的方程为.11.已知角的终边经过点(-3,4),则cos=;cos2=.12.如图,P为O外一点,PA是切线,A为切点,割线PBC与O相交于点B、C,且PC=2PA,D为线段PC的中点,AD的延长线交O于点E.若PB=,则·3·PA=;AD·DE=.13.现有6人要排成一排照相,其中甲与乙两人不相邻,且甲不站在两端,则不同的排法有种.(用数字作答)14.如图,正方形ABCD的边长为2,O为AD的中点,射线OP从OA出发,绕着点O顺时针方向旋转至OD,在旋转的过程中,记,OP所经过的在正方形ABCD内的区域(阴影部分)的面积S=f(x),那么对于函数f(x)有以下三个结论:①;②任意,都有·4·③任意其中所有正确结论的序号是.三、解答题:本大题共6小题,共80分.解答应写出必要的文字说明、证明过程或演算步骤.15.(本小题满分13分)在锐角△ABC中,角A,B,C所对的边分别为a,b,c,已知a=,b=3,.(Ⅰ)求角A的大小;(Ⅱ)求△ABC的面积.16.(本小题满分13分)某厂商调查甲、乙两种不同型号电视机在10个卖场的销售量(单位:台),并根据这10个卖场的销售情况,得到如图所示的茎叶图.为了鼓励卖场,在同型号电视机的销售中,该厂商将销售量高于数·5·据平均数的卖场命名为该型号电视机的“星级卖场”.(Ⅰ)当a=b=3时,记甲型号电视机的“星级卖场”数量为m,乙型号电视机的“星级卖场”数量为n,比较m,n的大小关系;(Ⅱ)在这10个卖场中,随机选取2个卖场,记X为其中甲型号电视机的“星级卖场”的个数,求X的分布列和数学期望.(Ⅲ)若a=1,记乙型号电视机销售量的方差为s2,根据茎叶图推断b为何值时,s2达到最小值.(只需写出结论)17.(本小题满分14分)如图1,在边长为4的菱形ABCD中,于点E,将△ADE沿DE折起到的位置,使,如图2.⑴求证:平面BCDE;⑵求二面角的余弦值;⑶判断在线段EB上是否存在一点P,使平面?若存在,求出的值;若不存在,说明理由.·6·18.(本小题满分13分)已知函数,其中aR.⑴当时,求f(x)的单调区间;⑵当a>0时,证明:存在实数m>0,使得对于任意的实数x,都有|f(x)|≤m成立.19.(本小题满分14分)设分别为椭圆E:的左、右焦点,点A为椭圆E的左顶点,点B为椭圆E的上顶点,且|AB|=2.⑴若椭圆E的离心率为,求椭圆E的方程;⑵设P为椭圆E上一点,且在第一象限内,直线与y轴相交于点Q,若以PQ为直径的圆经过点F1,证明:20.(本小题满分13分)·7·无穷数列P:,满足,对于数列P,记,其中表示集合中最小的数.(Ⅰ)若数列P:1‚3‚4‚7‚…,写出;(Ⅱ)若,求数列P前n项的和;(Ⅲ)已知=46,求的值.·8··9··10··11··12··13··14··15··16·